USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 2 - Várias Variáveis, Limites e Continuidade, Questão 1.4f
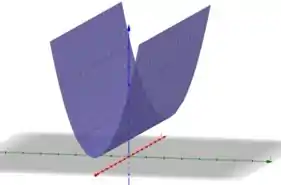
1.4. Esboce os gráficos de:
f.
Passo 1
Fala aí!! Bem-vindo! Está um pouco complicada essa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Nesse problema, nosso objetivo é obter o gráfico da função .
Tranquilo? 😉
Analisando a função, vemos que não varia, até porque nem está presente na função. Isso significa que se esboçarmos a função no plano , já vamos obter o gráfico em três dimensões.
Então podemos tratar a função inicialmente como bidimensional.
Bora começar! 😁
Passo 2
Se fizermos , vamos obter
Com isso vemos que a equação
É muito conhecida por nós, a diferença é que as variáveis estão trocadas.
Mas isso é fácil de resolver... em um plano cartesiano considerando o eixo das ordenadas como e o eixo das abcissas como , temos
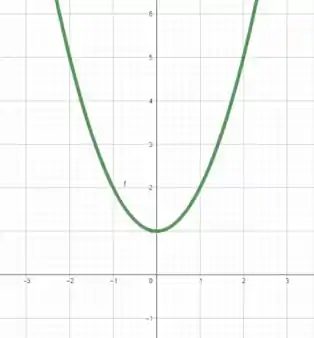
Assim, como é constante em todo o domínio, vamos obter que
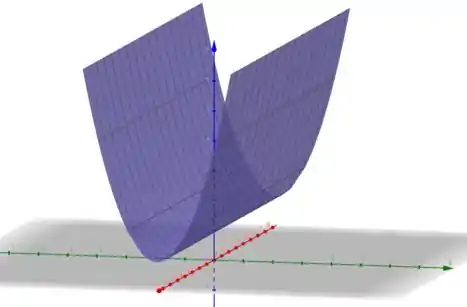
É isso! Essa resolução te ajudou? Responde Aí! ✌
Resposta
