USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 2 - Várias Variáveis, Limites e Continuidade, Questão 1.4k
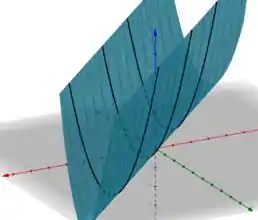
1.4. Esboce os gráficos de:
k.
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema, estamos interessados em obter o gráfico da função .
Parece de boa? 🤔
Para esboçar o gráfico de uma função tridimensional, podemos o método das seções...
Esse método consiste em fixar uma das variáveis a uma constante e obter uma curva bidimensional, assim, esboçando essa curva no plano onde fixamos a variável, podemos obter algumas “estruturas” do gráfico de .
Sacou como vai ser? 😁
Passo 2
Fazendo , vamos obter
Dessa forma, se definirmos constantes para , vamos obter parábolas com vértice em , por exemplo, se
Essa curva é uma parábola com vértice em
Se
Essa curva é uma parábola com vértice em
E para
Se trata de uma parábola com vértice em
Esboçando essas parábolas cada qual em seu plano em , vamos obter
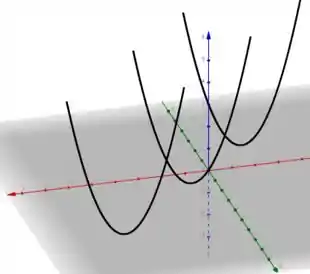
A partir daí podemos ter uma ideia de como a função se comporta
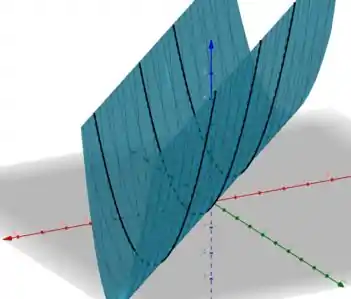
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
