USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 2 - Várias Variáveis, Limites e Continuidade, Questão 1.4m
1.4. Esboce os gráficos de:
m.
Passo 1
Iae, como vai? Essa questão está difícil, né? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nesse problema, estamos interessados em obter o gráfico da função .
Parece de boa? 🤔
Para esboçar o gráfico de uma função tridimensional, podemos o método das seções...
Esse método consiste em fixar uma das variáveis a uma constante e obter uma curva bidimensional, assim, esboçando essa curva no plano onde fixamos a variável, podemos obter algumas “estruturas” do gráfico de .
Sacou como vai ser? 😁
Passo 2
Fazendo , vamos obter
Manipulando essa equação, vamos chegar em
Dessa forma, vemos que se definirmos constantes para , em cada nível vamos obter uma elipse.
Por exemplo, para
Para
Para
E para
Bacana, não é? 😁
Passo 3
Esboçando cada curva em seu plano onde ele foi definido, vamos obter
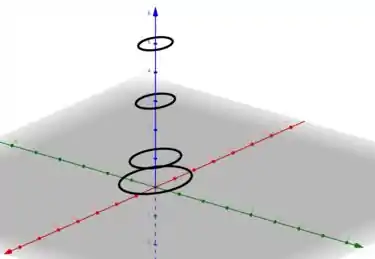
Ou seja, quanto menor , maior é a elipse... já quanto maior , menor é a elipse...
Assim podemos definir como a função se comporta ao longo de , veja só
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
Resposta
