USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 2 - Várias Variáveis, Limites e Continuidade, Questão 1.4p
1.4. Esboce os gráficos de:
p.
Passo 1
Iae! Como vai, meu querido? 😁 Bora aprender mais uma questão? 😉
Nesse problema, estamos interessados em obter o gráfico da função .
Parece de boa? 🤔
Para esboçar o gráfico de uma função tridimensional, podemos o método das seções...
Esse método consiste em fixar uma das variáveis a uma constante e obter uma curva bidimensional, assim, esboçando essa curva no plano onde fixamos a variável, podemos obter algumas “estruturas” do gráfico de .
Sacou como vai ser? 😁
Passo 2
Fazendo , vamos obter
Elevando os dois lados ao quadrado, vamos obter
Com isso, vemos que se definirmos valores para , vamos obter circunferências de raio .
Como inicialmente tínhamos a equação , só pode ser definido por valores positivos.
Por exemplo, para , temos
Para
Para
E para
Tudo certinho? 👀
Passo 3
Agora vamos esboçar cada circunferência obtida em seu devido plano de
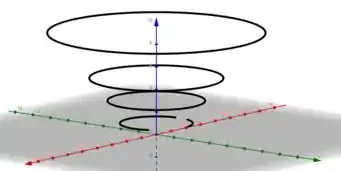
Assim, podemos imaginar como é o comportamento da função .
Esboçando seu gráfico, vamos obter
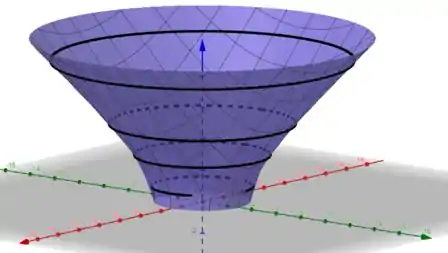
Pegou o esquema? Responde Aí! 😁
Resposta
