Esboce os gráficos das funções abaixo indicando: o domínio; as assíntotas, caso existam; os intervalos de crescimento e decrescimento; os extremos relativos e absolutos, caso existam; os intervalos onde o gráfico possui concavidade para cima e para baixo; os pontos de inflexão, caso existam.

Bom, vamos começar verificando o domínio de :

A única restrição está associada ao fato de ser uma fração em . Assim, o denominador precisa ser não-nulo, logo:

Portanto:

Vamos pensar nas assíntotas.

possui assíntotas horizontais, se:

Então, vamos verificar:

Resultado vale tanto para como para .

Logo, há uma assíntota horizontal em:

Já para as assíntotas verticais, sabemos que o nosso domínio não contém o ponto . Vamos verificar o que ocorre com nesse ponto:

Se , então .

Se então .

Portanto, temos uma assíntota vertical em .

Agora vamos verificar os intervalos de crescimento e decrescimento. Para isso, precisamos analisar os intervalos em que . Assim:

Daí, temos:

Ou seja:

Daí temos os intervalos de crescimento e decrescimento de .

Agora vamos calcular os extremos relativos e absolutos. Para isso, precisamos verificar os valores de que zeram a nossa :

Logo:

é a única solução.

Seria esse então o único o único ponto de máximo ou mínimo relativo. No caso, é um ponto de mínimo pois é negativo para imediatamente menor que .

E, é positivo para imediatamente maior do que .

Massa!

Quanto aos intervalos em que a função possui concavidade pra cima ou pra baixo, podemos calcular a segunda derivada de .

Logo:

Então, vamos ver os intervalos em que é positivo ou negativo:

Caso contrário, .

Ou seja:

Ponto de inflexão é justamente onde ocorre a mudança na concavidade da função.

Nesse caso então, vamos ter que:

É ponto de inflexão.

Agora sim, podemos finalmente esboçar o gráfico de .

Sabendo das assíntotas em , e das informações que obtivemos nos passos anteriores, podemos esboçar a seguinte curva:

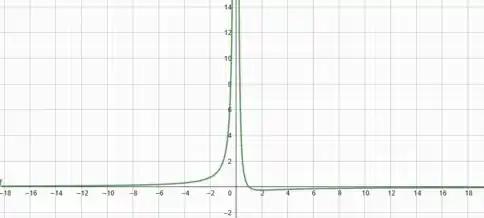
Prontinhooo!

Deu um trabalho, mas saiu 😊

Valeu pessoal, até a próxima!