UFPE, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Lista 2 de Exercícios, Questão 14c.
14. Esboce à mão o gráfico de e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de (nos domínios indicados).
c)
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nesse problema estamos interessados em esboçar a curva dentro de um intervalo e determinar os pontos de máximos e de mínimos da função.
Como vamos fazer isso? 🤔
Para obter o gráfico da função, podemos obter alguns pontos da função e estimar o comportamento dela dentro dos intervalos dos pontos.
Já para obter os pontos de máximo e mínimo, vamos calcular a derivada de e igualar a , assim, os pontos que satisfazerem a igualdade serão os pontos extremos. Mas caso eles não estejam no intervalo do domínio verificamos como se comporta.
Entendeu? Bora começar! 😁
Passo 2
Como e são duas retas, rica mais fácil plotar suas curvas, pois precisamos de apenas dois pontos em cada uma.
Vamos determinar a imagem de em , , e em .
Para
Para
Para
E para
Plotando esses pontos no plano cartesiano e estimando o comportamento de entre eles, temos algo mais ou menos como
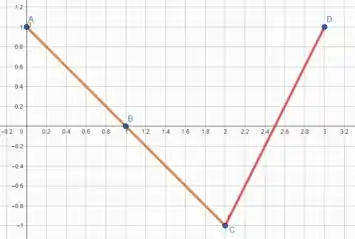
Tranquilo até aqui? 😊
Passo 3
Como é baseada em duas retas, então os pontos estremos serão os extremos do domínio.
Pelo gráfico, podemos ver que em , as duas retas se cruzam e dão origem ao ponto mínimo de .
Já em e em , é igual a , ou seja, temos dois valores máximos!
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
Resposta
, são pontos de máximos.
é ponto de mínimo.