UERJ, Sem Campus, Cálculo II, Listas de C2 - Profº Ditter Adolfo - 1ª Lista, Questão 3d
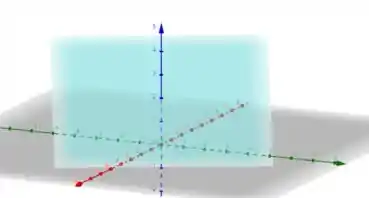
3) Esboce os seguintes planos:
(d) .
Passo 1
Iae, como vai? Essa questão está difícil, né? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nesse problema foi dada uma equação de um plano e nosso objetivo é esboçar o gráfico desse plano.
Sabe como fazer isso? 👀
Para esboçar um plano, precisamos de apenas três pontos... pra isso fazemos duas variáveis fixadas em e assim vemos em qual ponto o plano corta a variável que não foi fixada, ou seja, para encontrar o ponto em que o plano corta o eixo , fazemos e iguais a . Para obter o ponto em que o plano corta o eixo , fazemos e iguais a e assim sucessivamente.
Sacou? Bora começar! 😉
Passo 2
O plano foi dado como .
Vamos obter o ponto em que o plano corta o eixo fazendo
Agora para descobrir onde o plano corta o eixo , fazemos
E por fim, para saber onde o plano corta o eixo , fazemos
Com três pontos, podemos esboçar um plano, ou seja
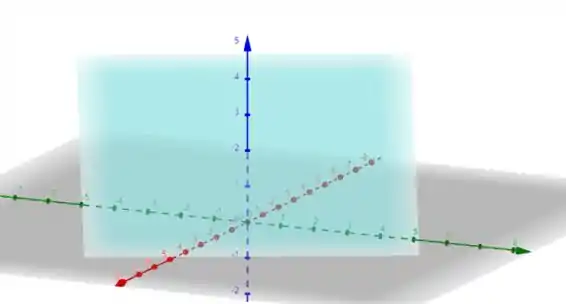
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
Resposta
