UNICAMP – Cálculo 1 – Lista 3 – Limite e Continuidade
18. Nos exercícios de a)-f), esboce o intervalo no eixo com o ponto dentro. Em seguida, determine um valor de , de modo que para todo ,
c)
Passo 1
Falaaa... tudo bem??
Nessa questão vamos esboçar, em um gráfico só do eixo , o intervalo dado e o ponto dentro. Depois vamos calcular um valor de de modo que se pertencer ao intervalo .
Passo 2
Esboçando o intervalo (lembrando que a bolinha é vazia, pois o intervalo é aberto:
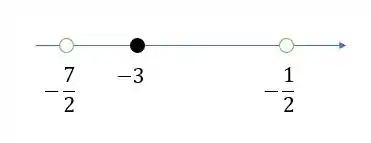
E a condição que precisa ser satisfeita é:
Repara que dentro do intervalo de -7/2 a -1/2 a condição é sempre satisfeita, exceto quando é igual a -3. Isso já é uma consequência do estar no meio do intervalo, então não precisamos nos preocupar com ela.
Passo 3
Usando o outro lado da condição:
Testando o primeiro extremo do intervalo:
Testando o outro extremo do intervalo:
Como precisa ser maior que 1/2 e maior que 5/2, então podemos escolher, por exemplo