UFU, Sem Campus, Cálculo 1, Profº Sato - Listas de Cálculo 1 - 1ª Lista de Exercícios, Questão 1.3a
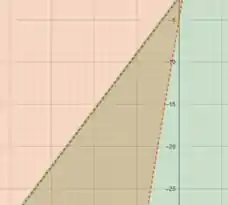
Se existir, faça um esboço da região do plano definida pelo sistema de desigualdades dados, nos seguintes casos:
e .
Passo 1
Faaala galerinha, tudo bom com vocês?
Nessa questão recebemos duas desigualdades:
E, precisamos esboçar a região determinada por essas inequações. Beleza?
Pra fazer isso precisamos conseguir entender que regiões essas desigualdades determinam no plano.
A dica é saber esboçar a reta associada a essas desigualdades. Podemos manipular essas equações até chegar em algo do tipo:
Isso significa que a região determinada por essa inequação é a região acima da reta
De forma análoga, se chegarmos em uma inequação do tipo:
É porque a região determinada é a que está abaixo da reta
Tranquilo? Então nossa estratégia vai ser primeiro determinar a reta associada a essas desigualdades e a partir disso determinar a região associada.
Vamo nessa!
Passo 2
Pra começar temos a inequação:
Daí, isolando vamos ter:
Assim, essa é a região abaixo da reta:
Vamos esboçá-la! Para isso basta determinar dois pontos da reta:
Daí:
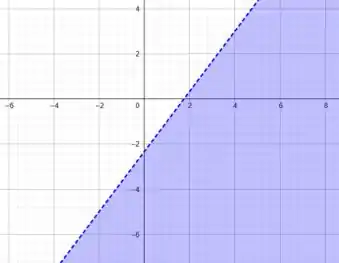
O tracejado é justamente a reta que determinamos anteriormente.
Vamos para a próxima desigualdade 😊
Passo 3
Agora temos:
Daí, isolando :
Ou seja, é a região superior à reta:
Para esboçar essa reta novamente basta determinarmos dois pontos que pertencem a ela. Assim:
Logo:
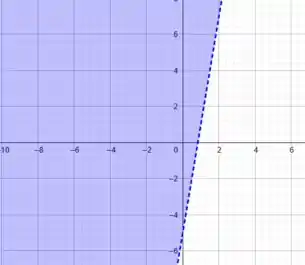
Excelente!
Passo 4
Agora precisamos apenas juntar esses esboços em uma mesma região pra determinar a intersecção entre essas áreas 😊
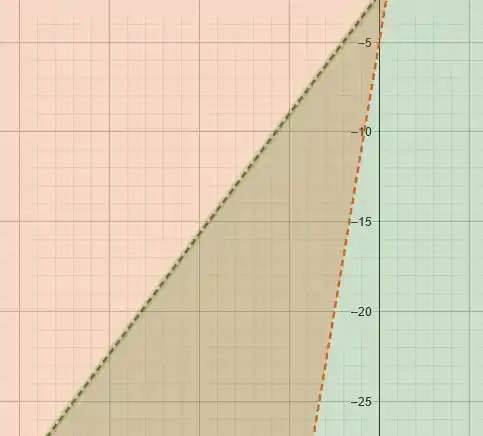
Perfeito galera! Essa região entre os tracejados é justamente a região definida no plano pelas desigualdades dadas no enunciado!
É isso então, até a próxima 😊
Resposta
