UFU, Sem Campus, Cálculo 1, Profº Sato - Listas de Cálculo 1 - 1ª Lista de Exercícios, Questão 1.3b
Se existir, faça um esboço da região do plano definida pelo sistema de desigualdades dados, nos seguintes casos:
Passo 1
E aí gente, tudo certinho?
Nessa questão recebemos uma inequação:
E, precisamos determinar a região do plano associada a essa inequação.
Pra fazer isso é essencial lembrarmos da correspondência entra alguns tipos de equação e as figuras que foram no plano.
No caso desse item, precisamos relembrar a equação da circunferência:
É a equação de uma circunferência centra em e com raio .
Tranquilo até aqui?
Então beleza, vamos dar uma olhada na inequação dada e tentar associar a uma figura plana conhecida 😊
Vem comigo!
Passo 2
Aqui tivemos uma promoção, pague uma inequação e leve duas haha. Pois:
Pode ser destrinchada como:
Pra conseguir entender melhor o que elas significam vamos considerar a situação de igualdade.
Se temos:
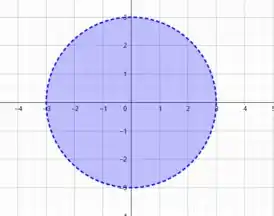
Trata-se da circunferência centrada em e com raio valendo .
Como temos o sinal de maior que significa que está sendo delimitada toda a região externa a essa circunferência.
Massa! Já na segunda inequação, analisando a igualdade temos:
Ou seja, uma circunferência centrada também em mas com raio . Só que, nesse caso temos um sinal de menor que, ou seja, estamos falando da região interna a essa circunferência.
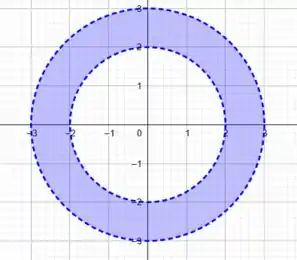
Fazendo a intersecção dessas duas regiões, vamos ter uma coroa circular, que podemos representar por:
Prontinho! Matamos mais uma questãozita 😊
Valeu pessoal!!
Resposta
