Se existir, faça um esboço da região do plano definida pelo sistema de desigualdades dados, nos seguintes casos:
e .
Passo 1
E aí pessoal, tudo tranquilo?
Nessa questão recebemos duas desigualdades:
E, precisamos esboçar a região determinada por essas inequações. Beleza?
Pra fazer isso precisamos conseguir entender que regiões essas desigualdades determinam no plano.
Uma ideia legal é analisar a igualdade dessas inequações. Daí, determinamos se trata de uma reta, uma circunferência, parábola. E, a partir disso, vemos o sinal da desigualdade pra determinar a região.
No caso desse item seria legal revisarmos as seguintes equações:
Massa! Sabendo disso, vamos colocar a mão na massa 😊
Passo 2
A começar pela primeira inequação, vamos isolar :
Analisando a igualdade agora, vamos ter:
Ou seja, a equação de uma parábola. Como essa parábola possui vértice em , e não possui raízes reais. Além disso, a parábola está virada pra cima . Como na inequação temos:
A região delimitada é abaixo da parábola. Vamos ter o seguinte esboço:
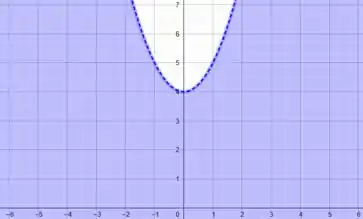
Perfeito!
Passo 3
Vamos analisar a próxima desigualdade, temos:
Isolando :
Se considerarmos a igualdade, temos a equação de uma reta. Para esboçá-la basta conhecermos dois pontos:
Como:
A região delimitada está acima da reta. Vamos ter o seguinte esboço:
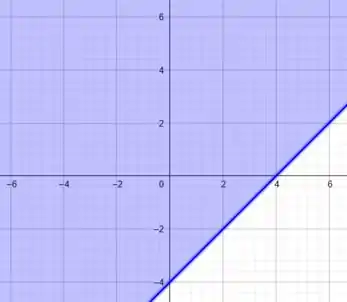
Daí, fazendo a intersecção das duas regiões, temos:
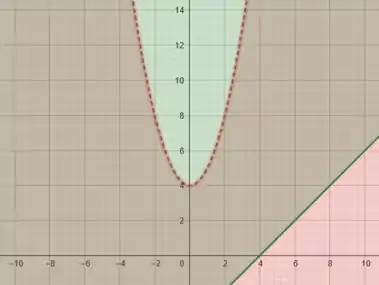
Ou seja, é toda a região acima da reta , exceto pela região dentro da parábola .
Show de bola!
Com isso matamos mais uma questão, obrigado pela atenção de vocês pessoal 😊
Resposta
Resposta no texto.