UFU, Sem Campus, Cálculo 1, Profº Sato - Listas de Cálculo 1 - 1ª Lista de Exercícios, Questão 1.3d.
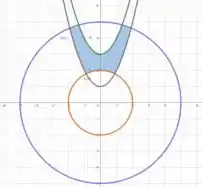
3. Se existir, faça um esboço da região do plano definida pelo sistema de desigualdades dados, nos seguintes casos:
(d) e .
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema, queremos obter a região definida pelas inequações e .
E aí, como fazemos isso? 🤔
Primeiro temos que buscar os limites dos gráficos e depois interpretar como a inequação está escrita, assim, hachurando a região dentro dos limites, obtemos as regiões que estamos procurando.
Bora lá! 😁
Passo 2
Olhando para a inequação , vemos que a região varia de até .
Perceba que essas equações são exatamente as equações da circunferência . Ou seja, essa região é definida entre a circunferência de raio e a circunferência de raio .
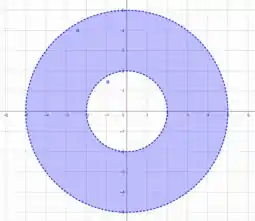
Tranquilo até aqui? 😊
Passo 3
Agora analisando a outra inequação, temos , ou seja, essa região varia entre e .
é a equação de uma parábola com a concavidade definida pelo sinal de . Como ambos são positivos, ambos possuem a concavidade voltada para cima.
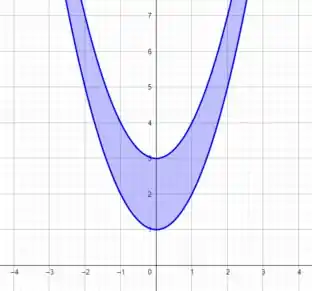
Bacana, não é? 😁
Passo 4
Por fim, se juntarmos as duas regiões em um único plano, vamos ter que a região que estamos procurando é
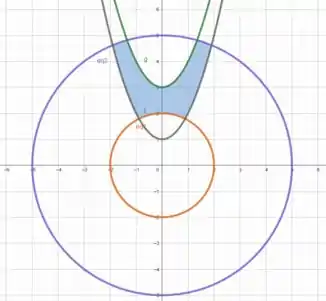
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
