UFU, Sem Campus, Cálculo 1 - Listas de Cálculo 1, Questão 5.3
Faça um esboço do gráfico de cada uma das inversas das seguintes funções trigonométricas (primeiro verifique qual é o domínio e imagem a dessas funções!): f (x) = cos (x), g (x) = sen (x ) e h (x) = tag (x )
Passo 1
Eaew, tudo certinho contigo?
Temos que fazer o esboço do gráfico de cada uma das inversas das funções trigonométricas:
, e
Além disso, temos que verificar qual o domínio e imagem dessas funções.
Vem comigo!
Passo 2
Primeiro vamos verificar o domínio e imagem das funções
, e
Para , o domínio é todo que pertence aos reais e sua imagem é ;
Para , o domínio é todo que pertence aos reais e sua imagem é ;
Para , o domínio é todo que pertence aos reais e sua imagem é .
Passo 3
Agora, vamos escrever as inversas
Para , inversa é ;
Para , inversa é ;
Para , inversa é .
Passo 4
Agora vamos esboçar os gráficos
:
:
:
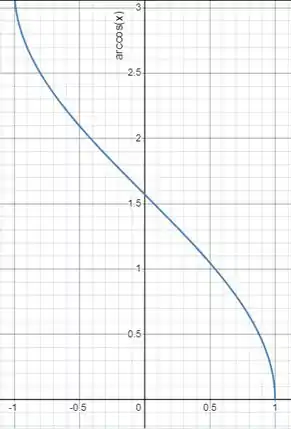
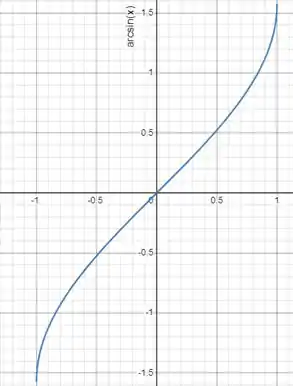
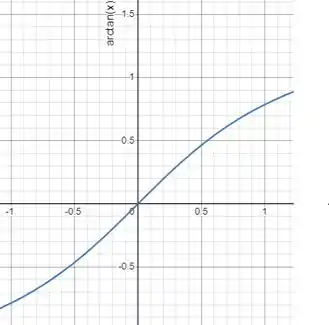
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
No decorrer da solução.