UFSCAR, Sem Campus, Cálculo 1, Listas de C1 - Profª Karla Spatti - Lista 5 - P2, Questão 5a
(a) Faça um esboço da representação geométrica dos planos cujas equações gerais são dadas por:
(i) x = 2; (ii) y + 1 = 0; (iii) z + 4 = 0; (iv) x − z = 0; (v) 2x + 3y + 4z − 12 = 0.
Passo 1
Eaew, belezinha?
O enunciado da questão define 5 planos e nos pede para fazer um esboço de cada superfície. Primeiro, comecemos com o caso (i), onde o plano é definido pela equação
Esse caso é bastante simples: a coordenada x de todos os pontos desse plano é igual à 2, enquanto y e z varia livremente. Então, esse plano é um plano paralelo ao plano yz, mas com coordenada x =2.
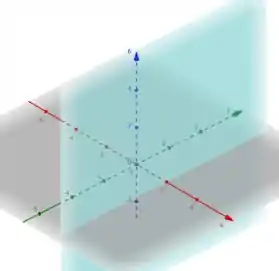
O plano (ii) é dado pela equação
Podemos reescrever essa equação como y = -1. O caso é parecido com o anterior, só que dessa vez é a coordenada y de todos os pontos do plano que é igual à -1, enquanto x e z varia livremente. Então, esse plano é um plano paralelo ao plano xz, mas com coordenada y = -1.
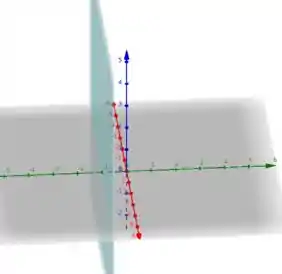
Para o terceiro caso temos a equação:
Podemos reescrever a equação como z = - 4. Mais uma vez temos o caso de um plano no qual as coordenadas z de todos os pontos do plano que é igual à -4, enquanto x e y varia livremente. Então, esse plano é um plano paralelo ao plano xy, mas com coordenada y = -4.
Agora, vamos dar uma olhada nos dois últimos casos que tem equações um pouco mais elaboradas. Então vamos lá!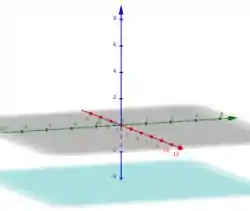
Passo 2
A equação do quarto plano é dada por
A equação acima só depende das variáveis x e z. Então, a gente já espera que, variando as coordenadas y, a nossa função não varia. Além disso, essa equação, é a equação de uma reta no plano xz com equação
Ou se,a. se olharmos planos xz, ao longo da direção y, teremos uma reta com inclinação igual à 1. A figura abaixo ilustra o plano.
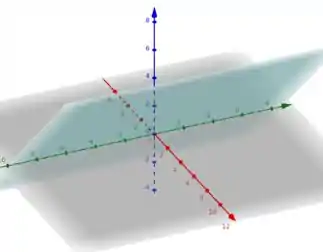
O quinto e último caso possui equação
A equação acima possui um termo de deslocamento igual a 12, mas o plano dado por essa equação é paralelo ao plano com equação
Se olharmos esse plano pelo eixo x, fazendo valores constantes, observamos funções do tipo
Essa equação representa uma reta decrescente entre z e y com inclinação
Se olharmos o plano pelo eixo y, fazendo valores constantes, observamos equações do tipo
Essa equação representa uma reta decrescente entre z e x com inclinação
Por fim, olhando o plano pelo eixo z, fazendo valores constantes, observamos no plano xy equações do tipo
Essa equação também é uma reta decrescente entre x e y com inclinação
Portanto, temos que o esboço do plano é da forma a seguir:
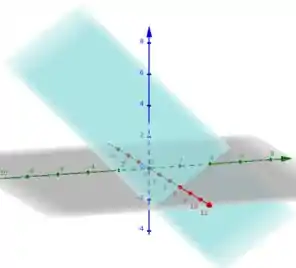
Resposta
Desenvolvida ao longo da questão.