USP, São Carlos, Calculo 2, Listas de C2 - Grupo Coordenado 2022 - Lista 3 - Módulo 3, Questão 1b
Faça o esboço do traço de cada curva parametrizada abaixo indicando a sua orientação:
(b)
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente esboçar a curva paramétrica e indicar sua orientação.
Pra isso, vamos transformar nosso vetor em uma equação cartesiana, usando as funções trigonométricas que ele nos deu. Assim, vamos conseguir identificar a forma da curva dada pelas equações paramétrica e plotá-la no gráfico cartesiano.
Vamos lá!
Passo 2
Lembra lá das coordenadas polares que tínhamos:
Pois bem, a única coisa que muda agora é a ordem e as constantes multiplicando as funções trigonométricas dadas em . Assim, temos:
A partir disso, usando a identidade trigonométrica , temos:
Repare que essa é a equação de uma elipse com eixo maior e eixo menor . Então podemos plotar nossa curva assim:
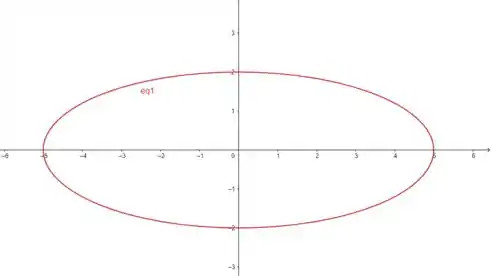
Pra definir a orientação da curva, precisamos perceber que o nosso intervalo vai de até . Então, substituindo esses extremos na equação paramétrica, temos:
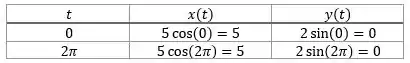
Então, nossa curva parte do ponto percorre a elipse no sentido anti-horário, positivo, e volta ao ponto .
Valeu, galera! Até a próxima! 😉