UFU – Cálculo 1 – Lista 1 – Questão 11c
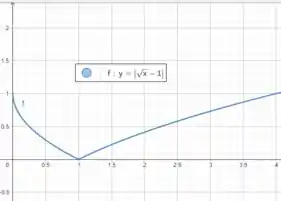
Faça o gráfico de cada função, sem marcar pontos, mas começando com o gráfico de uma das funções básicas elementares e então aplicando as transformações apropriadas
Passo 1
Oi pessoal, tudo bem? Vamos começar?
O problema começa nos dando uma função
E pediu para esboçar o gráfico sem marcar pontos! Ué! Como fazer isso?
Pensando em uma função primitiva muito parecida com essa! No nosso caso
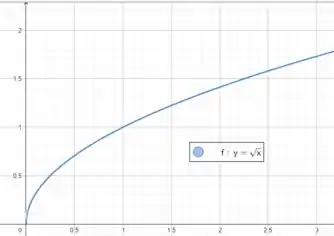
Partindo dessa função, precisamos reescrever a função dada na forma
e ir fazendo as transformações (no eixo com e no eixo com ). E o módulo? Depois de fazermos as transformações com e , vamos aplicar o módulo: tudo que está abaixo do eixo vamos esboçar acima!
Tudo que é negativo vira positivo! Isso que o módulo faz! É a última transformação a fazer!
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Nossa função é essa aqui
Vamos ter só transformação no deslocamento vertical com (descer uma unidade o gráfico todo)
Beleza?
E depois? Depois é o módulo!
Agora nossa missão é fazer aos poucos as transformações e ver como fica o gráfico final!
Passo 3
Nossa função é . Precisamos descer a raiz uma unidade para baixo:
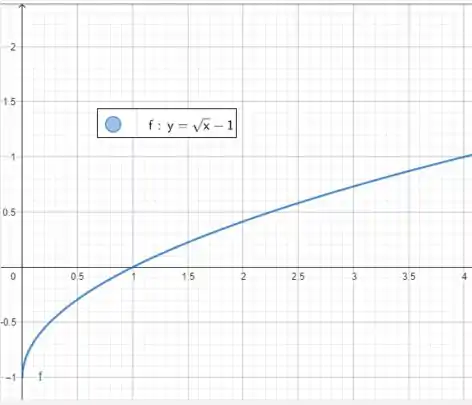
E agora tudo que está abaixo do eixo vamos rebater para cima!
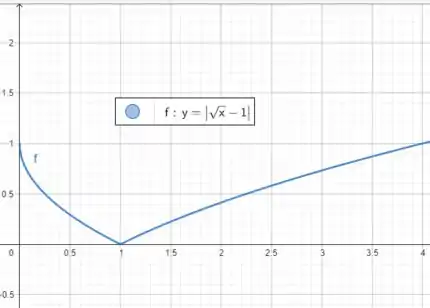
Beleza? Espero ter ajudado!
Até a próxima!
Resposta
