UNICAMP – Cálculo 1 – Lista 3 – Limite e Continuidade
26. Faça o gráfico da função e em seguida, responda:
b) Em quais pontos , se houver, existe?
Passo 1
Falaaa... tudo bem??
Nessa questão vamos dizer em quais pontos o limite de , com tendendo a , existe.
Pra isso, vamos lembrar que, pro limite existir, os limites laterais devem ser iguais.
Passo 2
Usando o gráfico:
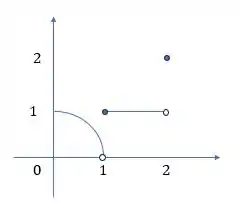
Repara que só vão ter limites laterais iguais nas “linhas” do gráfico. Então os pontos pertencem ao intervalo .
Repara que os valores dos extremos que são 0, 1 e 2 não pertencem ao intervalo, pois os limites laterais nesses pontos são diferentes.
Resposta
Exercícios de Livros Relacionados
Esboce a curva polar. r = s e n4 θ
Elimine o parâmetro para encontrar uma equação cartesiana da curva:Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta. x = senh t y = cosh t
Mostre que uma cônica com foco na origem, excentricidade e e diretriz y = d tem a equação polar r = e d 1 + e sen θ
Mostre que uma cônica com foco na origem, excentricidade e e diretriz y = - d tem a equação polar r = e d 1 - e sen θ
r = 9 6 + 2 cos θ (a) Encontre a excentricidade,(b) identifique a cônica,(c) dê uma equação da diretriz e(d) esboce a cônica