UTFPR, Sem Campus, Cálculo Diferencial e Integral 2, Listas de Cálculo 2 - Profº Ronie Peterson - Lista de Exercícios 1, Questão 3
Para a função , calcule e , determine e esboce o domínio e determine a imagem de .
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá uma função de duas variáveis , e nos pede algumas coisinhas.
Primeiramente devemos substituir e para descobrir e .
Por fim, devemos determinar e esboçar o domínio e a imagem de .
Não entendeu?? Vamos juntos!!
Passo 2
Bom... substituindo e para descobrir , temos:
Agora, substituindo e para descobrir , temos:
Passo 3
Assim, para o domínio de , temos:
Esboçando o domínio, temos:
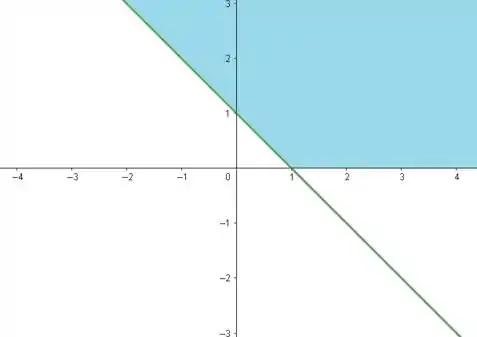
Passo 4
Assim, como é em sua essência uma função logarítmica, com base , então a imagem da função são todos os números em .
Entendeu direitinho? Responde aee ;)
Resposta
No texto
Exercícios de Livros Relacionados
Esboce a curva polar. r = s e n4 θ
Elimine o parâmetro para encontrar uma equação cartesiana da curva:Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta. x = senh t y = cosh t
Mostre que uma cônica com foco na origem, excentricidade e e diretriz y = d tem a equação polar r = e d 1 + e sen θ
Mostre que uma cônica com foco na origem, excentricidade e e diretriz y = - d tem a equação polar r = e d 1 - e sen θ
r = 9 6 + 2 cos θ (a) Encontre a excentricidade,(b) identifique a cônica,(c) dê uma equação da diretriz e(d) esboce a cônica