UFU, Sem Campus, Cálculo 1, Profº Sato - Listas de Cálculo 1 - 1ª Lista de Exercícios, Questão 9.2a.
2. O número de pessoas infectadas por uma epidemia de dengue é modelado por:
(a) Esboce o gráfico de .
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nessa questão temos que esboçar o gráfico da função dada por
Tranquilo? 🤔
Para esboçar o gráfico da função , podemos seguir alguns passos:
Primeiro verificamos o domínio da função: A expressão nunca é negativa, pois é a soma de um quadrado com uma constante positiva. Assim, o denominador nunca é zero. Portanto o domínio da função é todo o conjunto dos números reais.
Depois encontramos os interceptos com os eixos: Para encontrar o intercepto com o eixo , basta substituir por zero na expressão da função:
Assim, o gráfico passa pelo ponto .
Para encontrar o intercepto com o eixo , basta resolver a equação :
Isso só ocorre quando o numerador é zero, ou seja, quando . Portanto, o gráfico não intersecta o eixo .
Tranquilo até aqui? 😁
Passo 2
Depois disso temos que determinar os intervalos de aumento e redução: Para isso, podemos analisar o sinal da função em intervalos de . Para isso, observamos que o denominador é sempre positivo e que o sinal de é o mesmo que o sinal de .
Assim, temos:
Quando , temos , pois tanto o numerador quanto o denominador são positivos.
Quando , temos , pois o numerador e o denominador têm sinais opostos. Portanto, a função é crescente no intervalo e decrescente no intervalo .
Está acompanhando? 👀
Passo 3
E por fim, vamos determinar o comportamento assintótico: Para isso, podemos analisar o comportamento da função quando se aproxima do infinito ou do menos infinito. Observe que quando é muito grande em valor absoluto, o termo no denominador domina sobre os outros dois, tornando a função aproximadamente igual a . Portanto, a função tem uma assíntota oblíqua dada por , que é o eixo .
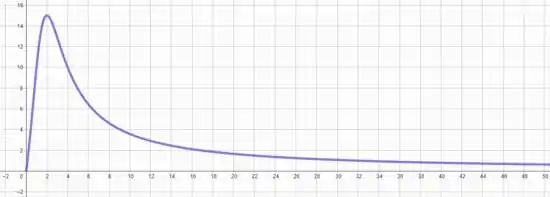
Portanto, para o gráfico de , esperamos que haja uma ascendência até onde e depois disso uma decadência com uma queda que vai suavizando quando se aproxima do eixo . Ou seja
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
Resposta
