UERJ, Sem Campus, Cálculo II, Listas de C2 - Profª Gabriela Coutinho - Lista 4, Questão 2c
Represente graficamente o domínio da função dada por:
c)
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente representar graficamente o domínio da função . Como essa é uma função de duas variáveis, nós precisamos encontrar a região do plano onde a função está definida, esse será o nosso domínio.
Para determinarmos e esboçarmos o domínio de uma função, devemos sempre garantir:
- nas frações o denominador não pode valer zero;
- dentro das raízes quadradas não pode ter número negativo;
- o valor dentro de um logaritmo tem que ser estritamente positivo.
Então, para esboçar o domínio da nossa função, vamos verificar as condições para que ela esteja definida.
Vamos lá!
Passo 2
Nossa função é dada por:
Nós temos duas raízes quadradas e sabemos que o que tem dentro delas precisa ser positivo, ou seja, maior ou igual a zero. Então, vamos ter as restrições:
E
Isolando as variáveis nas duas desigualdades, obtemos:
E
Isso quer dizer que nossa região está abaixo da reta e acima da parábola . Então, plotando a região no gráfico, vamos ter nosso domínio:
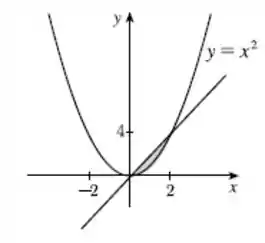
Valeu, galera! Até a próxima! 😉