UTFPR, Sem Campus, Cálculo Diferencial e Integral 1, Listas de Cálculo 1 - Profª Lilian Brambila - Lista 2 - Funções, Questão 5i
5. Sabe que, o módulo de um número real é definido da seguinte forma:
Com base nisso, dadas as funções em cada item, faça um esboço do gráfico de seu gráfico e encontre, se possível, sua imagem.
i)
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema foi dada uma função modular e nosso objetivo é esboçar seu gráfico e determinar sua imagem.
Tem ideia de como fazemos isso? 🤔
Aqui há três pontos importantes... primeiro: uma função modular não assume valores negativos, ou seja, se temos um valor , podemos reescrever simplesmente como , ignorando o sinal negativo.
O segundo ponto é que para esboçar o gráfico de uma função modular podemos esboçar a curva normalmente, mas espelhando o eixo pra cima.
E o terceiro ponto é que a imagem de uma função, é dada pelos possíveis valores para , ou seja, os possíveis valores que a função pode resultar.
Sacou? Bora começar! 👀
Passo 2
A função é dada por
Primeiro vamos esboçar o gráfico dessa função.
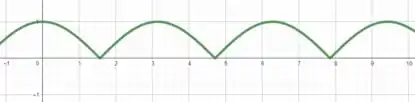
A função é uma função muito conhecida então temos que ter o gráfico dessa função decorado na cabeça, mas caso ainda não tenhamos chegado nesse nível, a função é uma função trigonométrica e periódica, ou seja, ela se repete ao longo do seu domínio.
Essa função passa em quando e se parece com uma onda variando entre e com um período de , ou seja, a cada intervalo de , ela se repete.
Então esboçando essas características em um gráfico, espelhando a parte negativa de para , vamos obter
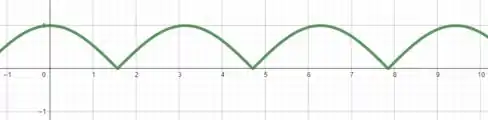
Tranquilo até aqui? 😁
Passo 3
E por fim, temos que determinar a imagem da função.
Perceba que o gráfico está contido no intervalo entre e , ou seja, a imagem de é dada por
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
