USP– Cálculo 1 – Lista 2 – Questão 1.6e
Seja uma função cuja derivada tem o gráfico esboçado na figura abaixo
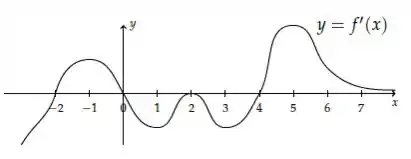
- Admitindo que , faça um esboço do possível gráfico de
Passo 1
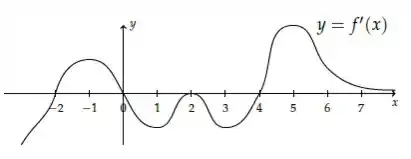
E agora pede para esboçarmos a função!
E agora, como fazer isso?
Nos itens anteriores encontramos os pontos onde a função é crescente/decrescente, onde tem máximo e mínimos locais, pontos de inflexão e concavidades positiva e negativa. Com isso podemos sim esboçar a função!
Os resultados encontrados foram:
E sabemos que
Então a ideia é usar todas essas características para formar nossa função!
Bora lá!
Passo 2
Agrupando todas as informações, uma função possível é essa aqui
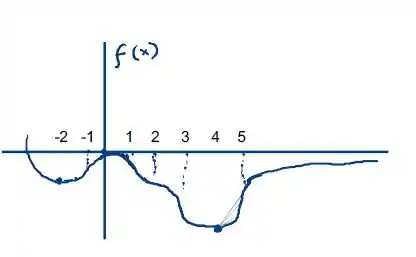
E é isso! Até a próxima!
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Esboce a curva polar. r = s e n4 θ
Elimine o parâmetro para encontrar uma equação cartesiana da curva:Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta. x = senh t y = cosh t
Mostre que uma cônica com foco na origem, excentricidade e e diretriz y = d tem a equação polar r = e d 1 + e sen θ
Mostre que uma cônica com foco na origem, excentricidade e e diretriz y = - d tem a equação polar r = e d 1 - e sen θ
r = 9 6 + 2 cos θ (a) Encontre a excentricidade,(b) identifique a cônica,(c) dê uma equação da diretriz e(d) esboce a cônica