UFCG, Sem Campus, Cálculo Diferencial e Integral I, 1º Estágio - 2016.1, Questão 1b
Seja a função definida por
b) Esboce o gráfico de .
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu uma função definida por partes, onde ela apresenta uma lei de formação diferente pra cada intervalo considerado, e nós precisamos esboçar o gráfico dessa função.
Vamos analisar cada intervalo e verificar o formato da curva correspondente a função naquele intervalo, beleza?
Vamos lá!
Passo 2
Olhando pra quando é menor do que , temos:
Então, nossa curva é uma reta constante horizontal igual a .
Quando é maior ou igual a e menor do que , temos a função:
Que é uma parábola deslocada em uma unidade para cima, com concavidade voltada para cima.
Agora quando tá entre e , a função tem a forma:
Que também representa uma reta crescente, mas que não está definida em .
Por fim, quando é maior ou igual a , , e temos uma reta horizontal constante em .
Juntando todas essas informações no gráfico, temos:
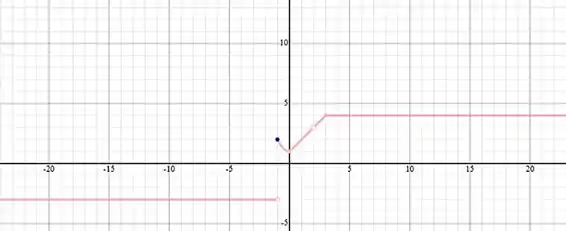
Valeu, galera! Até a próxima! 😉