Seja a interseção das regiões .
a) As fronteiras de respectivamente, são superfícies quádricas, identifique cada uma delas.
b)Faça um esboço da região
Passo 1
Identificando primeiramente
Se você for observar, essa é uma função que está escrita em função de x, y e z, certo? Isso nos indica ser no 3D, no entanto, se você for observar, temos nela somente x e y, certo? Então vamos plotar no plano xy mesmo.
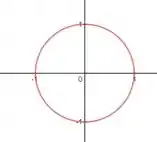
A função é uma muuuuito comum da gente trabalhar. Por isso vou te pedir pra você guardar ela no coração e lembrar que é um circulo bonitinho, tranquilo?
Bom, mas isso está no 2D, e agora? Bom, se na função não aparece a letra z, imagina que esse nosso desenho vá ser “esticado” na direção do eixo que eu n tenho. Daí vou ter isso:
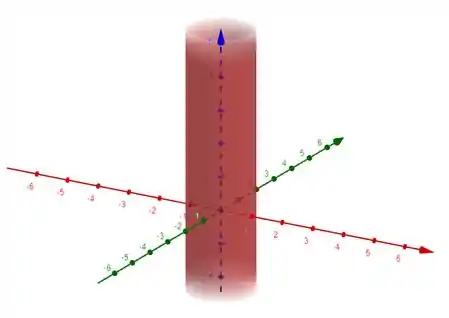
Pra concluir, observa ainda que temos . Esse nos indica que estamos trabalhando em valor menos que esse raio 1. Ou seja, a área trabalhada é a de DENTRO do cilindro. Tranquilo? Vem comigo pra essa próxima aqui então.
Passo 2
A fronteira de é pra mim a mais simples, onde estamos trabalhando simplesmente com valores acima do plano
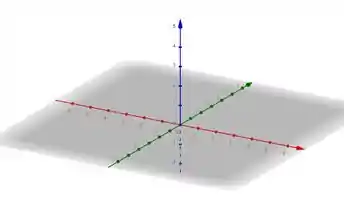
No desenho só destaquei pra gente o plano z=0. Ou seja, o plano onde todos os valores de z sempre vão ser zero, tranquilo? Só que nossa função é , ou seja, queremos então sempre z positivo! Logo, queremos tudo o que está acima desse plano....
Passo 3
Para a região temos.
Para essa função podemos reescrever como quando elevamos os dois lado da função ao quadrado. Logo, temos uma circunferência no eixo xy (lembra do olha ele seguindo a gente aí de novo). Dessa vez, o raio não é contante, ou seja, não é por exemplo. Agora temos , ou seja, o raio dessa circunferência do plano xy varia conforme a variação de z. Quanto maior o z, maior o raio. Então ele vai crescendo o raio junto com o z, o que nos dá:
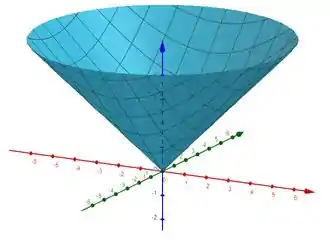
Passo 4
Esboçando então a região temos:
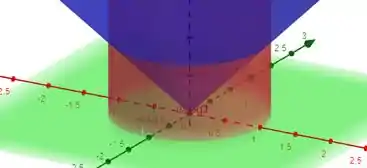
Onde a região estudada está acima do plano verde, dentro do cilindro e dentro do cone invertido.
Resposta
Ei, a resposta está no passo a passo :)