UFU, Sem Campus, Cálculo 1, Profº Sato - Listas de Cálculo 1 - 1ª Lista de Exercícios, Questão 2.3a.
Usando o conhecimento do gráfico de função , completamento de quadrados e as noções de deslocamento horizontal e vertical, trace um esboço do gráfico das seguintes funções:
(a)
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Nesse problema, temos que esboçar o gráfico da função mas principalmente temos que entender como funciona o deslocamento vertical dos gráficos.
Lembra como fazemos isso? 🤔
Quando temos uma parábola, com um vértice no ponto , temos uma função genérica dada por .
Mas se tivermos , o gráfico será muito parecido com o da função anterior, porém deslocado unidades verticalmente.
Se for positivo, o deslocamento aponta para cima e se for negativo, o deslocamento aponta para baixo.
Veja só!
Passo 2
Nesse exemplo, temos . Igualando essa função a uma função genérica do tipo , temos
Por igualdade de polinômios, chegamos em
Assim, na sua forma reduzida será
Como vimos anteriormente, esse gráfico é o mesmo que , porém deslocado unidades para baixo.
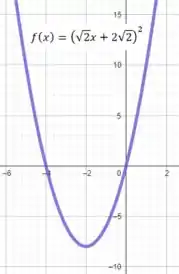
Viu só? Na esquerda está o gráfico de , já na direita o gráfico de
É isso! Essa resolução te ajudou? Responde Aí! ✌