UFU, Sem Campus, Cálculo 1, Profº Sato - Listas de Cálculo 1 - 1ª Lista de Exercícios, Questão 2.2b.
Usando o conhecimento do gráfico de função , da identidade dado pelo produto notável e a noção de deslocamento horizontal, trace um esboço do gráfico das seguintes funções:
(b) .
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema, temos que esboçar o gráfico da função mas principalmente temos que entender como funciona o deslocamento horizontal dos gráficos.
Lembra como fazemos isso? 🤔
Quando temos uma parábola, com um vértice no eixo , temos uma função genérica dada por .
Mas se tivermos , o gráfico será muito parecido com o da função anterior, porém deslocado unidades horizontalmente.
Se for positivo, o deslocamento aponta para a esquerda e se for negativo, o deslocamento aponta para a direita.
Veja só!
Passo 2
Nesse exemplo, temos a função
Se igualarmos a uma função genérica , então
Assim, por igualdade de polinômios vemos que
Logo, na sua forma reduzida é dada por
Lembra como é o gráfico de , então, nesse exemplo o gráfico será o mesmo, porém, deslocado unidades para a esquerda.
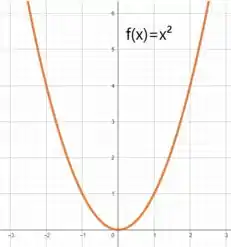
Viu só? Na esquerda está o gráfico de , já na direita o gráfico de
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍