Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 941234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939596979899100

Enunciado

Qual das alternativas abaixo exibe o valor correto da integral

∫ 0 1 ∫ 0 1 - x 2 e - x 2 + y 2 d y d x

Escolha uma:

a) π e 4

b) π + e 4

c) π 4 e

d) 4 π e

e) π e - 1 4 e

Passo 1

Cara, percebe que tem uma raiz no limite de integração e que tem o termo x 2 + y 2 , isso são dicas para usarmos coordenadas polares para resolver essa belezinha.

Usar coordenadas polares é fazer a mudança de variáveis:

x = r cos ⁡ θ ,     y = r   s e n   θ

x 2 + y 2 = r 2

Mas a gente precisa entender que região é essa do nosso domínio. A integral diz que:

0 ≤ y ≤ 1 - x 2

Repara que isso é o mesmo que dizer que y está entre y = 1 - x 2 e y = 0 . Repara com cuidado nessa primeira curva. Ela é a metade superior da circunferência

y = 1 - x 2 ∴ y 2 + x 2 = 1

Que está centrada em 0,0 e tem raio 1 .

E como a integral diz que 0 ≤ x ≤ 1 . Podemos desenhar nosso domínio como sendo essa região amarelinha:

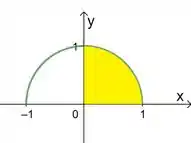
Passo 2

A gente precisa limitar r e θ para esse domínio.

Caminho 1: A gente precisa lembrar que r é o tamanho do segmento que sai da origem e vai até a borda do nosso círculo. Sendo assim, a gente pode escrever:

0 ≤ r ≤ 1

E lembrar que θ é o ângulo que sai no sentido anti-horário de x . Como nossa figura só está em um quadrante, θ vai só até π / 2 . Aí podemos dizer:

0 ≤ θ ≤ π 2

Passo 3

Agora é montar a integral. A gente já tem os extremos de integração, então vamos substituir nossa mudança de variáveis no integrando:

e - x 2 + y 2 = e - r 2

E aí a gente monta a integral, lembrando de multiplicar o integrando pelo fator r (que a gente chama de jacobiano dessa mudança).

I = ∫ 0 π 2 ∫ 0 1 e - r 2 r d r d θ

Passo 4

Vamos calcular o valor dessa nossa amiguinha. Usando a substituição:

u = - r 2 ,     d u d r = - 2 r ∴ d u - 2 = r   d r

u 1 = - 0 2 = 0

u 2 = - 1 2 = - 1

A integral fica:

I = ∫ 0 π 2 ∫ 0 - 1 e u - 2 d u d θ = ∫ 0 π 2 - e u 2 0 - 1 d θ = ∫ 0 π 2 - e - 1 2 + 1 2 d θ

I = ∫ 0 π 2 - 1 2 e + 1 2 d θ = ∫ 0 π 2 - 1 2 e + e 2 e d θ = π 2 - 1 2 e + e 2 e = π 4 e e - 1

Resposta

Letra e

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}