UFMG – Cálculo 3 – Lista 1 – Integrais duplas e triplas
2. Resolva as integrais duplas utilizando coordenadas polares:
a) em que é a parte do disco que está no primeiro quadrante e acima da reta .
Passo 1
Falaaa... beleza???
Nessa questão vamos calcular a integral dupla usando coordenadas polares, que é a mudança de variáveis:
E temos o Jacobiano:
E a integral dupla fica:
Passo 2
Vamos desenhar a região :
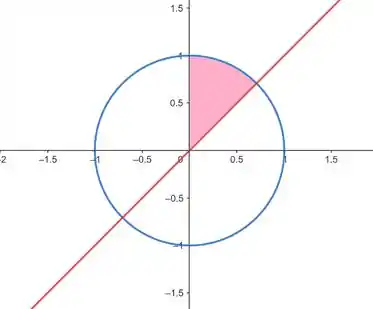
Então temos que vaia de até e, como é somente no primeiro quadrante e acima da reta, então varia de até .
Montando a integral dupla:
Passo 3
Usando substituição simples, podemos resolver a integral de dentro:
Os limites ficam:
Então:
Resposta
Exercícios de Livros Relacionados
Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}