Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 541234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFABC. Cálculo. Funções de Várias Variáveis. Lista 6 - Integrais Duplas. Questão 7b.

7 - Usando coordenadas polares, calcule:

b) ∫ - 1 1 ∫ - 1 - x 2 1 - x 2 1 - x 2 - y 2 d x d y

Passo 1

Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Estamos fazendo questões de integrais duplas e do nada aparece uma integral como essa, certamente vamos pensar “ferrou, vai dar muito trabalho e é capaz de eu nem conseguir fazer”.

E agora, o que fazer?

Existe uma técnica em que convertemos as coordenadas cartesianas x e y em coordenadas polares, onde x = r cos ⁡ θ e y = r s e n θ , com isso, onde tínhamos uma função f x , y vamos passar a ter f r , θ .

Isso também significa que como convertemos os valores em relação a r e θ , muitas vezes vamos ter uma simplificação também nos limites de integração.

Bora ver como vai ficar nossa integral? 😎

Passo 2

Antes de tudo, vamos definir nossa região de integração.

Vamos que em y , as curvas que nos limitam são 1 - x 2 e - 1 - x 2 e em x os limites ocorrem em 1 e - 1 .

Se plotarmos as curvas y = 1 - x 2 , y = - 1 - x 2 , x = 1 e x = - 1 , vamos obter

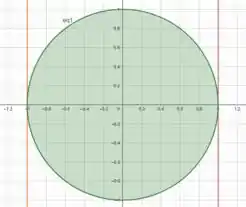
Vemos que temos um círculo de raio 1 . Esse indício é fundamental pra nos dizer que temos que aplicar a mudança para coordenadas polares.

Como y = ± 1 - x 2 , a região engloba a parte positiva e negativa de y , ou seja, o circulo completo. Sendo assim, nossos limites de integração em θ descreve a variação do ângulo de um círculo completo, ou seja, de 0 a 2 π . E se tratando de um círculo, seu raio varia de 0 a 1 .

Com os limites de integração encontrados, vamos ver nossa função f x , y = 1 - x 2 - y 2 , se fizermos 1 - x 2 - y 2 → 1 - x 2 + y 2 não mudamos nada na nossa função, não é?

Mas o que é x 2 + y 2 ? Pela equação da circunferência x 2 + y 2 = r 2 , logo

f r , θ = 1 - r 2

Tranquilo até aqui?

Passo 3

Substituindo essa função na nossa integral e aplicando os limites de integração, temos

∫ 0 1 ∫ 0 2 π 1 - r ² r d θ d r

Lembre-se de acrescentar o jacobino r multiplicando a função na integral!

Agora podemos calcular nossa integral.

Primeiro integrando com relação a θ :

Podemos perceber que não temos θ na nossa função, então 1 - r ² r se comporta como uma constante.

Sabemos que a integral de uma constante é a própria constante multiplicada pela variável de integração, ou seja

∫ 1 - r ² r d θ = 1 - r ² r θ

Aplicando os limites de integração, temos

∫ 0 2 π 1 - r ² r d θ = 2 π 1 - r ² r

A partir desse resultado, integramos com relação a r .

∫ 2 π 1 - r ² r d r → 2 π ∫ 1 - r ² r d r

Aplicando o método de substituição u d u sendo u = 1 - r ² .

Derivando u pela regra da cadeia, obtemos

d u d r = - 2 r · 1 2 1 - r 2

d r = - 1 - r 2 r d u

Substituindo u e d r

2 π ∫ u r - u r d u

2 π ∫ - u 2 d u

Tudo certo? 😁

Passo 4

Calculando a integral por meio da integração polinomial, onde dividimos a variável pela potencia + 1 e somamos 1 no seu expoente.

2 π ∫ - u 2 d u = 2 π - u 2 + 1 2 + 1 = - 2 π u 3 3

Substituindo u de volta 1 - r 2

2 π ∫ 1 - r ² r d r = - 2 π 1 - r 2 3 3

Aplicando os limites de integração, vamos obter o resultado final

∫ 0 1 ∫ 0 2 π 1 - r 2 r d θ d r = ∫ - 1 1 ∫ - 1 - x 2 1 - x 2 1 - x 2 - y 2 d x d y

∫ - 1 1 ∫ - 1 - x 2 1 - x 2 1 - x 2 - y 2 d x d y = - 2 π 1 - 1 2 3 3 - - 2 π 1 - 0 2 3 3

Organizando nosso resultado, temos

∫ - 1 1 ∫ - 1 - x 2 1 - x 2 1 - x 2 - y 2 d x d y = 2 π 3

É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍

Resposta

∫ - 1 1 ∫ - 1 - x 2 1 - x 2 1 - x 2 - y 2 d x d y = 2 π 3

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}