Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 371234567891011121314151617181920212223242526272829303132333435363839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFSCAR. Cálculo 3. Lista de Estudos – Integrais Duplas. Questão 4.

4 – Calcular:

∬ R   ( x 2 + y 2 ) d x d y

Em que R é a região interna à x 2 + y 2 = 4 y e externa à x 2 + y 2 = 2 y .

Passo 1

Fala aí! Tudo belezinha por aí? Vamos resolver mais essa questão juntos? Vem comigo!

Bem, o problema pediu pra gente calcular essa integral, que é uma integral dupla

∬ R   x 2 + y 2 d x d y

E disse que é pra gente fazer isso em R , que é a região interna à x 2 + y 2 = 4 y e externa à x 2 + y 2 = 2 y .

Bom, o primeiro passo será entender que região é essa, e para isso nós teremos que desenhá-la. Então bora fazer isso.

Passo 2

Vamos começar desenhando

x 2 + y 2 = 4 y

Perceba que essa é a equação de uma circunferência, e pra fazer as informações importantes aparecerem, temos que dar uma mexida nela. Vamos colocar o 4 y para o lado esquerdo da equação e completar os quadrados, ficando com:

x 2 + y 2 - 4 y = 0

Adicionamos 4 dos dois lados da equação para completar os quadrados

x 2 + y 2 - 4 y + 4 = 4

E teremos:

x 2 + ( y - 2 ) 2 = 4

Que é uma circunferência de raio 2 centrada em ( 0,2 ) .

Vamos fazer a mesma coisa do a segunda equação.

x 2 + y 2 = 2 y

x 2 + y 2 - 2 y = 0

x 2 + y 2 - 2 y + 1 = 1

E teremos:

x 2 + ( y - 1 ) 2 = 1

Que é uma circunferência de raio 1 centrada em ( 0 , 1 ) .

Desenhando as duas, teremos:

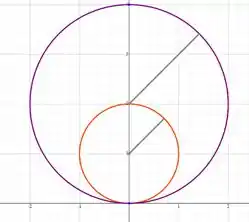
O problema disse pra gente que a região que teremos que integrar é interna à x 2 + y 2 = 4 y e externa à x 2 + y 2 = 2 y

Então devemos fazer a integral da região de forma, menos a integral da região de dentro. Ok

A R = A f o r a - A d e n t r o

Vamos encontrar essas áreas separadamente pra que tudo fique bem claro. Vem comigo.

Passo 3

Começando pela área de fora

∬ R   ( x 2 + y 2 ) d x d y

Na região limitada por x 2 + y 2 = 4 y

Usando as coordenadas polares, teremos:

x = r cos ⁡ θ

y = r sen ⁡ θ

J = r

E os limites de integração serão:

0 ≤ θ ≤ π

E para r , vamos lembrar que:

x 2 + y 2 = 4 y

Que pode ser escrito como

r 2 = 4   r sen ⁡ θ

r = 4 sen ⁡ θ

Assim,

0 ≤ r ≤ 4 sen ⁡ θ

E nossa integral será:

∫ 0 π ∫ 0 4 sen ⁡ θ r 2 r d r d θ

∫ 0 π ∫ 0 4 sen ⁡ θ r 3 d r d θ

Resolvendo, teremos

∫ 0 π r 4 4 | 0 4 sen ⁡ θ d θ

∫ 0 π 64 sen 4 ⁡ θ d θ

Essa integral é bem chatinha de resolver. Vamos segurar ela aqui um pouquinho e ver o que está acontecendo na outra região também pra fazê-la uma vez só. Ok.

Passo 4

Agora vamos olhar a área de dentro

∬ R   ( x 2 + y 2 ) d x d y

Na região limitada por x 2 + y 2 = 2 y

Usando as coordenadas polares, teremos:

x = r cos ⁡ θ

y = r sen ⁡ θ

J = r

E os limites de integração serão:

0 ≤ θ ≤ π

E para r , vamos lembrar que:

x 2 + y 2 = 2 y

Que pode ser escrito como

r 2 = 2   r sen ⁡ θ

r = 2 sen ⁡ θ

Assim,

0 ≤ r ≤ 2 sen ⁡ θ

E nossa integral será:

∫ 0 π ∫ 0 2 sen ⁡ θ r 2 r d r d θ

∫ 0 π ∫ 0 2 sen ⁡ θ r 3 d r d θ

Resolvendo, teremos

∫ 0 π r 4 4 | 0 2 sen ⁡ θ d θ

∫ 0 π 4 sen 4 ⁡ θ d θ

Percebeu que a integral é muito parecida. Então vamos ajustar tudo de uma vez só.

Passo 5

Fazendo

A R = A f o r a - A d e n t r o

Teremos:

A R = 64 ∫ 0 π sen 4 ⁡ θ d θ - 4 ∫ 0 π sen 4 ⁡ θ d θ

A R = 6 0 ∫ 0 π sen 4 ⁡ θ d θ

Agora vamos resolver a integral

∫ 0 π sen 4 ⁡ θ d θ

Que pode ser escrita com:

∫ 0 π sen 2 ⁡ θ 2 d θ

Lembrando que sen 2 ⁡ θ = 1 - cos ⁡ 2 θ 2

∫ 0 π sen 2 ⁡ θ 2 d θ = ∫ 0 π 1 - cos ⁡ 2 θ 2 2 d θ

Resolvendo a potência, ficamos com:

1 4 ∫ 0 π ( 1 - 2 cos ⁡ 2 θ + cos 2 ⁡ 2 θ )   d θ

Lembrando que cos 2 ⁡ 2 θ = 1 + cos ⁡ 4 θ 2

1 4 ∫ 0 π ( 1 - 2 cos ⁡ 2 θ + cos 2 ⁡ 2 θ )   d θ = 1 4 ∫ 0 π ( 1 - 2 cos ⁡ 2 θ + 1 2 + cos ⁡ 4 θ 2 )   d θ

E

1 4 ∫ 0 π ( 1 - 2 cos ⁡ 2 θ + 1 2 + cos ⁡ 4 θ 2 )   d θ = 1 4 ∫ 0 π ( 3 2 - 2 cos ⁡ 2 θ + cos ⁡ 4 θ 2 )   d θ

Integrando tudo, ficamos com:

1 4 ∫ 0 π ( 3 2 - 2 cos ⁡ 2 θ + cos ⁡ 4 θ 2 )   d θ = 1 4 3 θ 2 - 2 sen ⁡ 2 θ 2 + 1 2 sen ⁡ 4 θ 4 | 0 π

Aplicando os limites de integração:

1 4 3 π 2 - 2 sen ⁡ 2 π 2 + 1 2 sen ⁡ 4 π 4 - 1 4 3 ⋅ 0 2 - 2 sen ⁡ 2 ⋅ 0 2 + 1 2 sen ⁡ 4 ⋅ 0 4 = 3 π 8

Assim, concluímos que

∫ 0 π sen 4 ⁡ θ d θ = 3 π 8

Mas lembra que a gente deixou um 60 lá atrás? Então vamos buscá-lo.

A R = 60 ∫ 0 π sen 4 ⁡ θ d θ = 60 ⋅ 3 π 8 = 45 π 2

E finalmente, integral resolvida.

Depois dessa, toma uma aguinha e volta pra gente continuar. Ok?!

Resposta

∬ R   ( x 2 + y 2 ) d x d y = 45 π 2

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}