UFABC. Cálculo. Funções de Várias Variáveis. Lista 6 - Integrais Duplas. Questão 7a.
7 - Usando coordenadas polares, calcule:
a) , onde ;
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Para obter a integral dessa questão, temos que converter nossas variáveis para coordenadas polares. Fazemos isso como um método pra facilitar nossos cálculos, muito provavelmente se tentássemos calcular essa integral pelo método que tínhamos aplicado até agora, seria muito mais difícil.
Mas como vamos aplicar coordenadas polares? 🤔
A ideia é substituir as coordenadas cartesianas pelas coordenadas polares, lembra?
Com isso, ao invés de integrarmos com relação a e , vamos integrar com relação a e .
Fazendo essas substituições, podemos ter uma integral muito mais simples.
Bora ver?
Passo 2
Primeiro de tudo, vamos desenhar a região no plano cartesiano pra definir e .
Vemos que representa um círculo de raio e nos diz que estamos interessados em valores de positivos.
Plotando essas curvas, podemos ver que a hachura mais escura é a parte que estamos interessados.
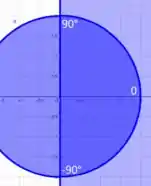
Como vimos, nosso vai de a , então nossos limites de integração em são esses.
Sempre consideramos o semieixo positivo de como referência para o ângulo . Partindo do maior para o menor ângulo, vemos que temos uma variação de até , concorda?
Então nossos limites de integração em é de a . Lembrando que sempre temos que descrever os ângulos em radianos na integral.
Por falar na nossa integral. ⚠🛑❌ ATENÇÃO! Nunca esqueça de acrescentar o jacobiano quando converter uma integral para integral polar!
Com isso, nossa integral será
Mas ainda temos que modificar nossa função de integração. Observando a função, vemos que por conta da equação da circunferência, então substituindo, vamos obter
Simplificando um pouquinho, temos
Agora sim!
Passo 3
Percebeu como está mais clean a integral agora?
Primeiro vamos integrar com relação a , assim se comporta como uma constante. Como não temos na nossa função, sabemos que a integral de uma constante é a própria constante multiplicada pela variável de integração.
Agora integramos com relação a . Por integração polinomial, dividimos a variável pela sua potência e somamos no seu expoente.
Dessa forma, obtermos o resultado da nossa integral como !
É isso! Essa resolução te ajudou? Responde Aí! ✌
