b) Calcule a integral

Considerando

Agora precisamos identificar os novos intervalos de integração. Vamos analisar novamente o esboço que fizemos ao resolver a letra a) dessa questão (no Capítulo 2):

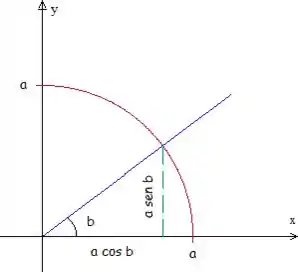
O limite superior é . Se elevarmos os dois lados ao quadrado, passamos a ter:

Essa é a equação de uma circunferência de raio . Como a raiz tem que ser positiva, vamos desenhar apenas a parte com .

A outra equação que limita é , que nada mais é do que uma reta de coeficiente angular igual a , que desenhamos acima em azul.

Agora vamos analisar os limites de : temos e , ou seja, dois números. Mas não é um valor qualquer de , é exatamente o ponto em que a reta corta a circunferência, pois:

Assim, o ponto satisfaz as duas equações.

Vemos, então, que em coordenadas polares podemos descrever essa região dessa forma:

Pra cobrir toda a região, o raio tem que variar de a e o ângulo de a .

Antes de substituir tais valores na integral do problema, perceba que:

Isso vai ajudar a simplificar a integral porque teremos: .

Agora vamos integrar em relação a ;

Antes de integrar em relação a , vamos aplicar a equação trigonométrica:

Caso você não se lembrasse dessa fórmula, poderia utilizar as equações do arco duplo: e , só teria um pouquinho mais de trabalho.

Assim, temos: