Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 213456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Calcule ∬ D   l n ⁡ ( x 2 + y 2 )   d x d y , onde D é a região do primeiro quadrante situada entre as circunferências x 2 + y 2 = 1 e x 2 + y 2 = 4 .

Passo 1

Para resolver essa integral dupla, nós precisamos encontrar os limites de integração. Repara que o enunciado disse a região que estão integrando esta delimitada por no primeiro quadrante de duas circunferências. Sendo assim, é uma boa usar coordenadas polares para definirmos esses limites.

A mudança de coordenadas polares que faremos será:

x = r cos ⁡ θ

y = r sen ⁡ θ

Lembrando, que qualquer mudança de variável, implica em multiplicar a função da integral pelo Jacobiano. Nas coordenadas polares, o Jacobiano dessa transformação sempre será J = r .

Passo 2

Agora vamos analisar os intervalos de integração! O enunciado forneceu duas equações:

x 2 + y 2 = 1

x 2 + y 2 = 4

A primeira corresponde a uma circunferência de raio igual a 1 . Já a segunda, é uma circunferência de raio igual a 2 .

O problema também diz que a região está limitada no primeira quadrante. Então a região que estamos estudando será essa abaixo:

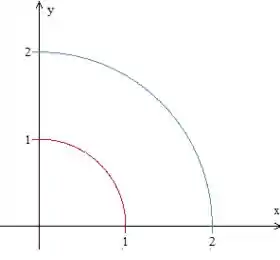
Repara que o raio r varia entre 1 e 2 e o ângulo θ entre 0 e π / 2 .

Passo 3

Agora que encontramos os limites de integração, vamos substituir na integral. Lembrando que a integral que estamos resolvendo tem essa cara:

∬ D   l n ⁡ ( x 2 + y 2 )   d x d y

Vamos, então, montar a integral, substituindo os valores que atribuímos a x e y :

∫ 1 2   ∫ 0 π 2 ln ⁡ r cos ⁡ θ 2 + r sen ⁡ θ 2 r d θ d r =

∫ 1 2   ∫ 0 π 2 r ln ⁡ r 2 ⁡ d θ d r

Não podemos esquecer o Jacobiano. Esse r que está multiplicando a função vem do Jacobiano!

Passo 4

Agora partiu resolver a integral!

∫ 1 2   ∫ 0 π 2 r ln ⁡ r 2 ⁡ d θ d r

Vamos começar integrando em relação a θ :

= ∫ 1 2   r ln ⁡ r 2 θ θ = 0 θ = π / 2 d r =

= π 2 ∫ 1 2 r ln ⁡ r 2   d r =

Mas ln ⁡ r 2 = 2 ln ⁡ r . Então, no fim, fica:

= π 2 ∫ 1 2 2 r ln ⁡ r   d r

= π ∫ 1 2 r ln ⁡ r   d r

Passo 5

Para integrar em relação a r , vamos fazer a integração por partes, com:

ln ⁡ r = u

r = v '

O que nos dá:

u ' = 1 r

v = r 2 2

Substituindo esses valores em ∫ u v ' = u v - ∫ u ' v

Temos:

∫ r ln ⁡ r d r = r 2 2 ln ⁡ r - ∫ 1 r × r 2 2 d r = r 2 2 ln ⁡ r - r 2 4

Então, o valor da nossa integral é:

π ∫ 1 2 r ln ⁡ r   d r = π r 2 2 ln ⁡ r - r 2 4 r = 1 r = 2 =

= π 4 2 ln ⁡ 2 - 4 4 - 1 2 ln ⁡ 1 - 1 4 =

= π 2 ln ⁡ 2 - 1 + 1 4 =

π 2 ln ⁡ 2 - 3 4

Resposta

π 2 ln ⁡ 2 - 3 4

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}