Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 811234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980828384858687888990919293949596979899100

Enunciado

Coordenadas Polares

Considere a região plana

R = x , y ∈ R 2 x 2 + y 2 - x ≤ 0 , x 2 + y 2 - y ≥ 0 , y ≥ 0

E a integral dupla

I = ∬ R x 2 + y 2 d x d y

  1. Esboce a região plana R
  2. Seja C 1 a parte da fronteira de R que está contida na circunferência de equação x 2 + y 2 - x = 0 e C 2 a parte da fronteira de R que está contida na circunferência de equação x 2 + y 2 - y = 0 . Descreva C 1 e C 2 nos seguintes formatos:

    3. C 1 = x , y ∈ R 2 y = f 1 x ,     a ≤ x ≤ b

    C 2 = x , y ∈ R 2 x = f 2 y ,     c ≤ y ≤ d

    Explicitando as constante a , b , c e d e as funções f 1 e f 2

  3. Descreva a região plana R utilizando coordenadas polares, no seguinte formato:

    4. g θ ≤ r ≤ h θ ,     α ≤ θ ≤ β

    Explicitando as funções g e h e as constantes α e β

  4. Calcule a integral dupla I utilizando o método que preferir.

Passo 1

Vamos começar entendendo a região R , temos duas equações de circunferência, vamos olhar a primeira delas

x 2 + y 2 - x = 0

Completando quadrados

x 2 - x + 1 4 + y 2 = 1 4

x - 1 2 2 + y 2 = 1 4

Isso é uma circunferência de raio 1 2 e centro em 1 2 , 0

Vamos ver a segunda

x 2 + y 2 - y = 0

Completando quadrados

x 2 + y 2 - y + 1 4 = 1 4

x 2 + y - 1 2 2 = 1 4

Isso é uma circunferência de raio 1 2 e centro em 0 ,   1 2

O gráfico dessa bagunça vai ser assim

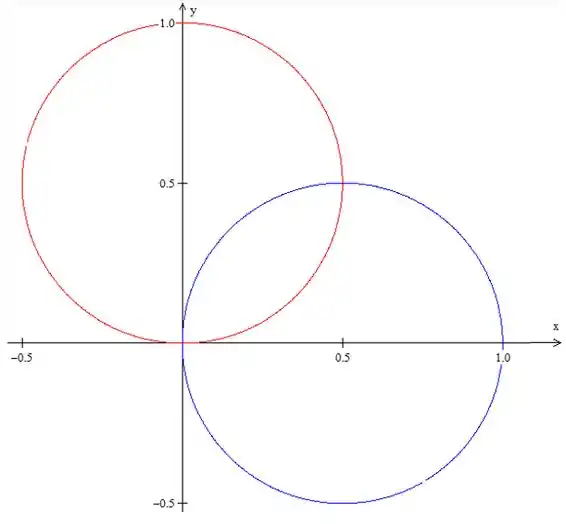
A circunferência em vermelho é x 2 + y - 1 2 2 = 1 4 e a em azul é x - 1 2 2 + y 2 = 1 4 .

Vamos entender agora as desigualdades, primeiro ele diz que y ≥ 0 , então esquece tudo que está embaixo do eixo x , depois ele disse

x 2 + y 2 - x ≤ 0

Que na verdade é

x - 1 2 2 + y 2 ≤ 1 4

Que é a parte de dentro da circunferência azul.

Depois ele disse que

x 2 + y 2 - y ≥ 0

Que na verdade é

x 2 + y - 1 2 2 ≥ 1 4

Que é a parte de fora da circunferência vermelha.

O gráfico da região R vai ser

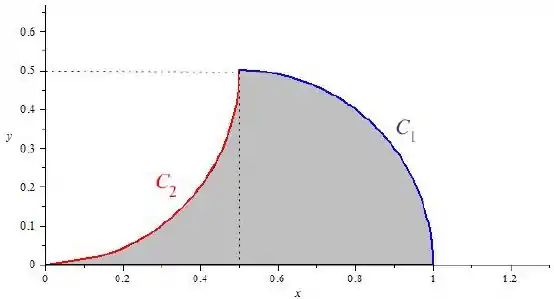
Passo 2

b )

Vamos escrever as fronteiras, começando com C 1 , que é da circunferência

x - 1 2 2 + y 2 = 1 4

Aqui ele quer y = f 1 x , e o intervalo de x , o intervalo de x podemos tirar pela figura, vai ser

1 2 ≤ x ≤ 1

A função é só pegar a equação da circunferência e isolar o y

x - 1 2 2 + y 2 = 1 4

⇒ y 2 = 1 4 - x - 1 2 2

⇒ y = ± 1 4 - x - 1 2 2

Como estamos com y > 0 vamos ter

y = 1 4 - x - 1 2 2

Vamos ter

C 1 = x , y ∈ R 2 y = 1 4 - x - 1 2 2 ,   1 2 ≤ x ≤ 1

Passo 3

Vamos agora para C 2

Aqui ele quer x = f 2 y , e o intervalo de y , o intervalo de y podemos tirar pela figura, vai ser

0 ≤ y ≤ 1 2

A função é só pegar a equação da circunferência e isolar o x

x 2 + y - 1 2 2 = 1 4

⇒ x 2 = 1 4 - y - 1 2 2

⇒ x = ± 1 4 - y - 1 2 2

Como estamos com x > 0 vamos ter

x = 1 4 - y - 1 2 2

C 2 = x , y ∈ R 2 x = 1 4 - y - 1 2 2 ,     0 ≤ y ≤ 1 2

Passo 4

c )

Vamos ver agora em coordenadas polares, lembrando que as coordenadas ficam

x = r cos ⁡ θ

y = r sen ⁡ θ

Passo 5

Temos que achar os intervalos do θ e do r , o ângulo vai começar no 0 e vai até a junção das duas circunferências, vamos ver uma figura para entender como ver esse ângulo.

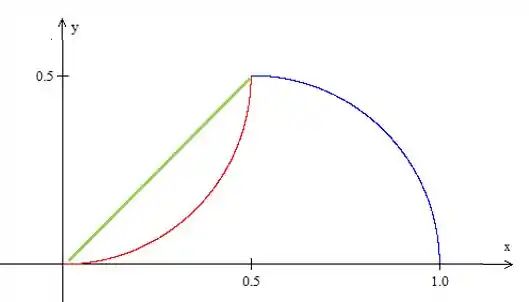
Consegue ver que a reta verde vai ter inclinação de π 4 ? Isso por que vamos ter

tan ⁡ θ f = 0,5 0,5 = 1

E pronto o ângulo final é π 4

Temos que ver agora os valores do raio, ele vai de uma circunferência até a outra. Começando com a vermelha

x 2 + y 2 - y = 0

Substituindo os valores das coordenadas polares

r cos ⁡ θ 2 + r sen ⁡ θ 2 - r sen ⁡ θ = 0

r 2 cos 2 ⁡ θ + sen 2 ⁡ θ - r sen ⁡ θ = 0

r 2 - r sen ⁡ θ = 0

r = sen ⁡ θ

Temos o valor inferior de r , vamos ver na outra circunferência para achar o valor superior de r

x 2 + y 2 - x = 0

Substituindo os valores das coordenadas polares

r cos ⁡ θ 2 + r sen ⁡ θ 2 - r cos ⁡ θ = 0

r 2 cos 2 ⁡ θ + sen 2 ⁡ θ - r cos ⁡ θ = 0

r 2 - r cos ⁡ θ = 0

r = cos ⁡ θ

Então vamos ter

R = r , θ ∈ R 2 sen ⁡ θ ≤ r ≤ cos ⁡ θ , 0 ≤ θ ≤ π 4

Passo 6

d )

Vamos fazer a integral, como temos x 2 + y 2 na integral vamos usar coordenadas polares, eu não coloquei ali em cima, mas precisamos lembrar que

J = r

A integral vai ficar

I = ∬ R r cos ⁡ θ 2 + r sen ⁡ θ 2 r d r d θ = ∬ R r 2 cos 2 ⁡ θ + sen 2 ⁡ θ r d r d θ

I = ∬ R r 2 r d r d θ = ∬ R r 3 d r d θ

Colocando os limites de integração

I = ∫ 0 π / 4 ∫ sen ⁡ θ cos ⁡ θ r 3 d r d θ

I = ∫ 0 π / 4 r 4 4 r = sen ⁡ θ cos ⁡ θ d θ = ∫ 0 π / 4 cos ⁡ θ 4 4 - sen ⁡ θ 4 4 d θ =

Usando produtos notáveis vamos ter

I = ∫ 0 π / 4 cos ⁡ θ 2 2 - sen ⁡ θ 2 2 cos ⁡ θ 2 2 + sen ⁡ θ 2 2 d θ

I = ∫ 0 π / 4 cos ⁡ θ 2 2 - sen ⁡ θ 2 2 1 2   d θ

Vamos colocar esse 1 2 do seno e do cosseno em evidência

I = 1 2 1 2   ∫ 0 π / 4 cos ⁡ θ 2 - sen ⁡ θ 2   d θ = 1 4   ∫ 0 π / 4 cos ⁡ θ 2 - sen ⁡ θ 2   d θ

Lembrando das propriedades de cosseno vamos ter

cos ⁡ 2 θ = cos 2 ⁡ θ - sen 2 ⁡ θ

Arrumando essa integral vamos ter

I = 1 4   ∫ 0 π / 4 cos ⁡ 2 θ   d θ = 1 4 sen ⁡ 2 θ 2 θ = 0 π / 4 = 1 4 sen ⁡ 2 π 4 2 - sen ⁡ 2.0 2

I = 1 4 sen ⁡ π 2 2 - sen ⁡ 0 2 = 1 4 1 2 - 0 = 1 4 1 2 = 1 8

Resposta

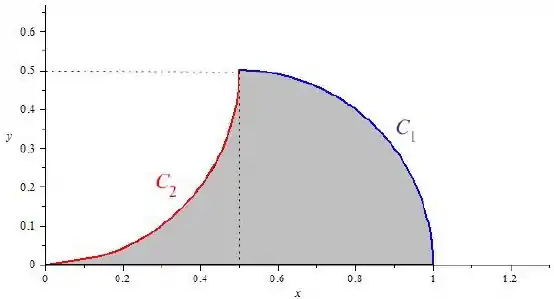
  1. C 1 = x , y ∈ R 2 y = 1 4 - x - 1 2 2 ,   1 2 ≤ x ≤ 1

    2. C 2 = x , y ∈ R 2 x = 1 4 - y - 1 2 2 ,     0 ≤ y ≤ 1 2

  2. R = r , θ ∈ R 2 sen ⁡ θ ≤ r ≤ cos ⁡ θ , 0 ≤ θ ≤ π 4
  3. I = 1 8

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}