Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 101123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Questão 1: Calcule a integral

∬ R   x 2 + y 2   d x d y

Onde R é a região limitada pela desigualdade x 2 + y - 1 2 ≤ 1 .

Passo 1

Antes de sairmos jogando o algebrismo no papel, vamos desenhar essa região R aí:

“Onde R é a região limitada pela desigualdade x 2 + y - 1 2 ≤ 1 ”

Veja que se trata de um círculo de raio 1 deslocado uma unidade e em y :

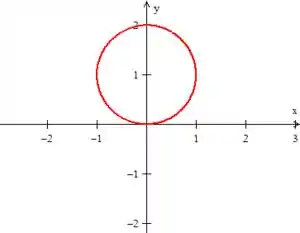
Passo 2

Como se trata de uma região circular, e estamos integrando x 2 + y 2 , é uma boa pensarmos em uma mudança para coordenadas polares:

x = r cos ⁡ θ

y = r sin ⁡ θ

J = r

E, somando x 2 com y 2 , chegamos à equação do círculo que é muito importante pra gente aqui:

x 2 + y 2 = r 2

Passo 3

Bem, precisamos agora descrever a nossa região R , em termos das coordenadas polares. Nessa mudança que fizemos (mudança de coordenadas para polares clássicas), o θ sempre gira a partir do eixo x ...

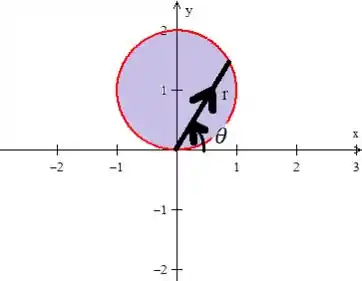
Logo, para formar a nossa região R , ele tem girar até 180 ° ...

0 ≤ θ ≤ π

Enquanto isso, o nosso r varia da origem até a circunferência...

0 ≤ r ≤ c i r c u n f e r ê n c i a

Como a equação da circunferência é...

x 2 + y - 1 2 = 1               →                     r cos ⁡ θ 2 + r sin ⁡ θ - 1 2 = 1                 →

r 2 cos 2 ⁡ θ + r 2 sin 2 ⁡ θ - 2 r sin ⁡ θ + 1 = 1               →

r 2 cos 2 ⁡ θ + sin 2 ⁡ θ - 2 r sin ⁡ θ = 0               →

r 2 - 2 r sin ⁡ θ = 0               →

r 2 = 2 r sin ⁡ θ               →

r = 2 sin ⁡ θ

Logo...

0 ≤ r ≤ 2 sin ⁡ θ

Passo 4

Logo, a gente pode voltar para integral dupla, onde a gente pode substituir tudo, inclusive, não podemos esquecer-nos de colocar o Jacobiano multiplicando a função...

∬ R   x 2 + y 2   d x d y = ∫ 0 π ∫ 0 2 sin ⁡ θ r 2 ⋅ J   d r d θ =

∫ 0 π ∫ 0 2 sin ⁡ θ r ⋅ r   d r d θ = ∫ 0 π ∫ 0 2 sin ⁡ θ r 2   d r d θ

Calculando a integral de dentro...

∫ 0 π ∫ 0 2 sin ⁡ θ r 2   d r d θ = ∫ 0 π r 3 3 0 2 sin ⁡ θ d θ =

∫ 0 π 2 sin ⁡ θ 3 3 d θ =

8 3 ∫ 0 π sin 3 ⁡ θ d θ = 8 3 ∫ 0 π sin ⁡ θ ⋅ sin 2 ⁡ θ d θ =

8 3 ∫ 0 π sin ⁡ θ ⋅ 1 - cos 2 ⁡ θ d θ = 8 3 ∫ 0 π sin ⁡ θ - sin ⁡ θ cos 2 ⁡ θ d θ =

Calculando essa integral...

8 3 - cos ⁡ θ + cos 3 ⁡ θ 3 0 π = 8 3 - cos ⁡ π + cos 3 ⁡ π 3 - - cos ⁡ 0 + cos 3 ⁡ 0 3 =

8 3 - - 1 + - 1 3 - - 1 + 1 3 = 8 3 1 - 1 3 + 1 - 1 3 =

8 3 4 3 = 32 9

Resposta

32 9

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}