UFABC. Cálculo. Funções de Várias Variáveis. Lista 6 - Integrais Duplas. Questão 7d.
7 - Usando coordenadas polares, calcule:
d) , onde é a região limitada por
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Quando temos uma integral dupla, onde a região de integração é na forma circular ou elíptica, converter as coordenadas para polares nos ajuda muito já que muitas vezes é quase impossível obter o resultado e os intervalos de integração por meio das coordenadas cartesianas.
Mas como fazemos para converter uma integral para as coordenadas polares? 🤔
De forma bem direta, para fazer essa mudança, temos que fazer umas substituições. Primeiro com relação a função de integração , temos que muda-la para . Pra isso, onde tem , substituímos por e onde tem por .
Também temos que mudar os limites de integração quando derivamos em relação a , temos que adotar os limites de integração para os valores de maior ângulo e de menor ângulo com relação ao semieixo positivo de que fazem parte da região .
E na integral com relação a temos que adotar como limites de integração os valores de m
Passo 2
Primeiro vamos ver como é nossa região de integração. Manipulando a equação, podemos chegar em
Com isso, temos a seguinte região
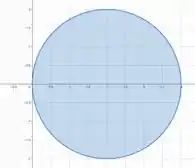
As perguntas que devemos fazer agora é: “Qual o maior e o menor ângulo que a região faz com a origem do sistema tendo como ângulo o semieixo positivo de ?”.
A outra pergunta é: “Como o raio da região varia com o ângulo ?”
Analisando a região, vemos que o maior e o menor ângulo que ela faz é e respectivamente.
Podemos perceber que a variação do raio não é constante, conforme o ângulo muda, o raio também muda.
Se convertermos a equação que delimita para polar, temos
Como
Descobrimos que varia de a , então esses serão nossos limites de integração
Passo 3
Convertendo nossa função para , temos
Com isso, finalmente temos a integral
Não se esqueça de acrescentar o jacobiano na integral.
Integrando com relação a , aplicamos o método de integração polinomial onde dividimos a variável pela potência e somamos no seu expoente
Aplicando os limites de integração
Agora derivamos esse resultado com relação a
Como é uma constante pode sair da integral
Tranquilo até aqui?
Passo 4
Integrando pelo método de integração por partes, temos
Onde e
Com isso, temos que obter a integral
Podemos reescrever essa integral como
Sabemos que a integral de uma constante é a própria constante multiplicada pela variável de integração, já a integral de é obtida pelo método de integração por substituição
Substituindo na integral de , temos
Aplicando os limites de integração.
Para
Para
Um pouquinho trabalhoso, não é? 😅
Passo 5
Dessa forma, a integral com os limites de integração aplicados é
Simplificando o resultado, temos
Fim! Iae, o que achou? Responde Aí! 😁
