Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 861234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848587888990919293949596979899100

Enunciado

UFMG – Cálculo 3 – Lista 1 – Questão 8

Calcule a seguinte integral

∬ D e x 2 e y 2 d A

Em que D é a região limitada pelas retas y = 3 x e y = 0 e pela circunferência x 2 + y 2 = 4 , no terceiro quadrante

Passo 1

Oi pessoal, tudo bem? Vamos começar?

O problema começa nos dando essa integral iterada

∬ D e x 2 e y 2 d A = ∬ D e x 2 + y 2 d A

E pediu para calcular essa integral usando coordenadas polares. E agora, o que fazer? Nossa pergunta de milhões precisa de uma resposta de milhões...

Fazendo um desenho da região! Pegando a região dada temos

x 2 + y 2 = 4

y = 3 x  

y = 0  

No terceiro quadrante!

E esboçando essa região, temos isso aqui

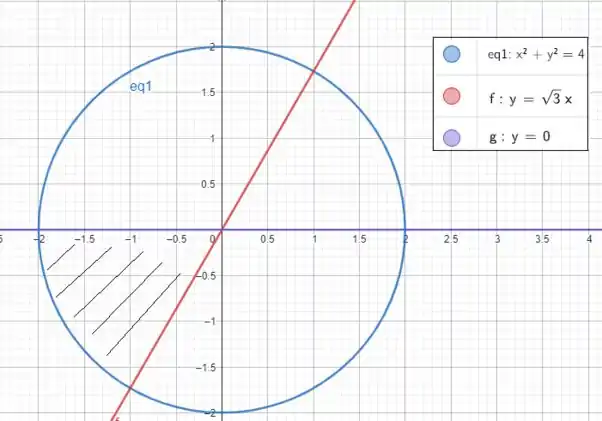
Percebemos que a região é um setor circular! Os limites em r vão de 0 até 2 e em θ de π (da reta y = 0 ,   no terceiro quadrante) até 4 π 3 (que é o ângulo que faz π 6 + π , região do terceiro quadrante que a reta y = 3 x corta)

Lembrando que o diferencial de área em polares é

d A = r   d r   d θ

Agora é só trocar o integrando para coordenadas polares e integrar!

Mas relaxa, vou fazer passo a passo com você!

Passo 2

A integral que precisamos resolver é essa

∬ D e x 2 + y 2 d A

Já temos os limites de integração em polares

0 ≤ r ≤ 2

π ≤ θ ≤ 4 π 3

Agora falta nosso integrando! A relação entre as coordenadas cartesianas e polares é

x = r c o s   θ

y = r   s e n θ

Aí nosso integrando fica

x 2 + y 2 = r 2 s e n 2 θ + r 2 cos 2 ⁡ θ = r 2

Bora montar essa integral!

∫ π 3 π 4 ∫ 0 2 e r 2 r   d r   d θ

Beleza?

Agora nossa missão é resolver essa integral!

Passo 3

Nossa integral é essa aqui

∫ π 3 π 4 ∫ 0 2 e r 2 r   d r   d θ

Integrando em r e substituindo os limites de integração:

u = r 2 → d u = 2 r   d r

Quando r = 0 ,   u = 0 , quando r = 2 ,   u = 4 :

∫ π 3 π 4 e u 2 0 4 d θ = ∫ π 3 π 4 e 4 2 - 1 2 d θ

Tranquilo? Agora vamos resolver essa integral em θ !

Assim temos

= e 4 2 - 1 2   θ π 3 π 4 = e 4 2 - 1 2 . 3 π 4 - π

Simplificando

= 1 - e 4 π 8

Beleza? Espero ter ajudado!

Até a próxima!

Resposta

1 - e 4 π 8

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}