Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 321234567891011121314151617181920212223242526272829303133343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Use coordenadas polares para calcular a área da região R interior ao círculo x - 1 2 + y 2 = 1 , exterior ao círculo x 2 + y 2 = 1 .

Passo 1

Vamos primeiramente tentar entender essa região que nós estamos trabalhando, ok?

Observa que ele nos diz que a região está no interior de x - 1 2 + y 2 = 1 ,   que é um círculo de raio 1 deslocado uma unidade no eixo x

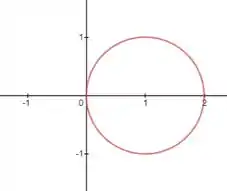
Sabemos ainda também que a região se encontra no exteriordo círculo x 2 + y 2 = 1 .

O que nos leva então a essa região

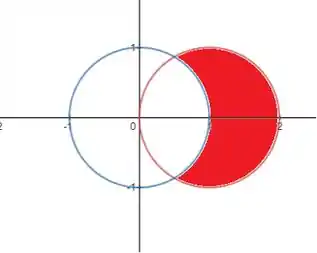
Passo 2

Precisamos lembrar ainda que nas coordenadas polares, nossas substituições serão

x = r c o s θ

y = r s e n θ

E temos que lembrar ainda do Jacobiano, que nos vai ser dado por

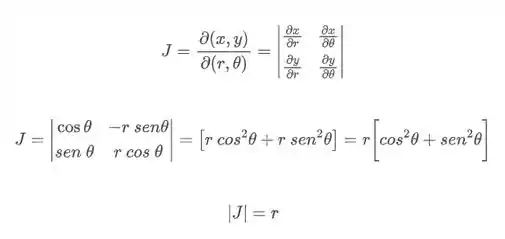
Passo 3

Substituindo nas equações que temos

x 2 + y 2 = 1 .

r 2 cos 2 ⁡ θ + r 2 s e n 2 θ = 1

r 2 s e n 2 + cos 2 ⁡ θ = 1

r = 1

Até aí tranquilo. Fazendo o mesmo na outra equação

x - 1 2 + y 2 = 1

r c o s θ - 1 2 + r 2 s e n 2 θ = 1

r = 2 c o s θ

Com isso temos a variação do raio, que sabemos sair da circunferência centrada na origem ( r = 1 ) e ir até a deslocada ( r = 2 c o s θ ) .

Passo 4

Já o θ vai vairar entre os pontos onde as circunferências se encontram, ou seja

x - 1 2 + y 2 = x 2 + y 2

x 2 - 2 x + 1 = x 2

- 2 x + 1 = 0

x = 1 2

r c o s θ = 1 2

q u a n d o   r = 1

c o s θ = 1 2

O cosseno é igual a 1 2 quando θ vale ± π 3

Logo

- π 3 ≤ θ ≤ π 3

1 ≤ r ≤ 2 c o s θ

Passo 5

Nosso último passo agora então é montar e calcular nossa integral

A = ∫ - π 3 π 3 ∫ 1 2 c o s θ r   d r   d θ

Observa que isso nos desenha toda a áre vermelha

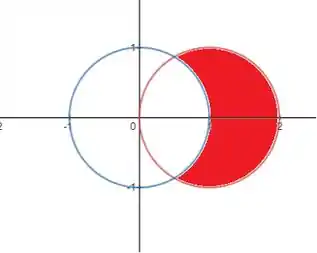
Mas observa como ela é simplesmente espelhada no eixo x. Então, pra fazer nossas continhas mais simples, vou escrever

A = 2 ∫ 0 π 3 ∫ 1 2 c o s θ r   d r   d θ

O que significa basicamente que se eu tiver duas metades de cima, eu numericamente tenho a mesma área que procuramos.

∫ 0 π 3 ( 4 cos 2 ⁡ θ - 1 )   d θ

Vamos substituir cos 2 ⁡ θ = 1 + c o s 2 θ 2

∫ 0 π 3 4 1 + c o s 2 θ 2 - 1 d θ

= π 3 + 3 2

Resposta

π 3 + 3 2

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}