UFABC. Cálculo. Funções de Várias Variáveis. Lista 6 - Integrais Duplas. Questão 7c.
7 - Usando coordenadas polares, calcule:
c) , onde é a região limitada por e .
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Temos uma integral para resolver, dada por
Onde é a região limitada entre as duas equações e .
Se tentássemos calcular essas integrais pelo método convencional, íamos ter um enorme trabalho.
Mas então como vamos calcular esse negócio??
Observando a região , vemos que ela é limitada por duas circunferências, isso é um indício que temos que converter os valores de e para coordenadas polares.
Lembra como fazemos isso? 🤔
Passo 2
Primeiro de tudo vamos identificar nossa região de integração e definir nossos limites de integração.
Desenhando nossas curvas e , temos
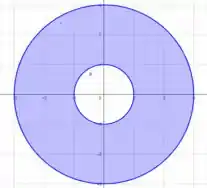
Só de ver esse gráfico já bateu uma fome de donuts, não é? 😋
Quando temos a região de integração na forma de circular ou elíptica, temos que observar duas coisas.
A primeira a variação angular que a região faz com a origem do sistema e a variação do raio da circunferência.
Como a região leva em consideração o anel completo, a variação angular usando sempre como base o semieixo positivo é de a
Já a variação do raio é a distância mínima e máxima da região com a origem. Vemos que o limite mínimo é dado quando estamos sob a circunferência , ou seja, quando o raio é igual a . Já o limite máximo é dado quando estamos sob a circunferência , ou seja, quando o raio é igual a (raio = ).
Com isso, os limites de integração de é dado por
Mas e aí, agora é só calcular a integral?
Passo 3
Calma, já vamos poder calcular essa integral, mas ainda falta uma coisinha.
Nossa função é dada por , mas temos que converter para coordenadas polares .
Para converter para polares, temos que substituir e , ou no caso, como temos , substituímos simplesmente por . Só lembrar da equação da circunferência .
Agora sim, substituindo essa função na nossa integral sem esquecer do jacobiano !
Primeiro integrando com relação a , vemos que não temos na nossa função então se comporta como uma constante.
Como sabemos a integral de uma constante é a própria constante multiplicada pela variável de integração.
Aplicando os limites de integração, temos
Agora temos que usar o resultado dessa integral pra integrar com relação a
Passo 4
Agora temos a integral
Por integração de polinômios, dividimos a variável pela sua potência e somamos no seu expoente.
Se aplicarmos os limites de integração, temos
Logo, nossa resposta é
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
