Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 781234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677798081828384858687888990919293949596979899100

Enunciado

UFSCAR, Sem Campus, Cálculo 3, Listas de C3 - Profª Alessandra Verri - Lista 3, Questão 2g

Por meio de coordenadas polares, encontre o volume do sólido Q

Q : a c i m a   d o   c o n e   z = x 2 + y 2   e   a b a i x o   d a   e s f e r a   x 2 + y 2 + z 2 = 1

Passo 1

Fala aí galera, bora resolver o nosso exercício? Vamos começar fazendo um esboço da nossa região delimitada.

C o n e :   z = x 2 + y 2

E s f e r a : x 2 + y 2 + z 2 = 1

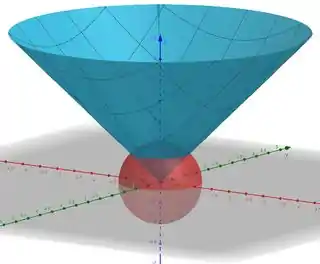
Mas para termos uma ideia da variação de x e y , vamos ter que analisar como fica no plano x y . Para isso, temos que achar os pontos de intercepção das duas superfícies:

x 2 + y 2 + z 2 = 1

x 2 + y 2 + x 2 + y 2 = 1 → x 2 + y 2 = 1 2

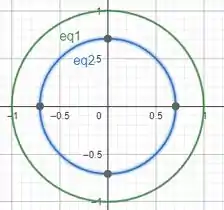
Como queremos trabalhar com coordenadas polares, vamos dizer:

x = r c o s θ

y = r s e n ( θ )

J = r

Show, com essas informações, a gente vai conseguir calcular.

Passo 2

Para começar, vamos começar trazendo a equação da integral:

V = ∬ R f x , y d A

Temos que achar a nossa f x , y . Para isso, temos que usar as equações do enunciado:

x 2 + y 2 + z 2 = 1 → z = 1 - x 2 - y 2

z = x 2 + y 2

Como o volume que a gente quer é a intercepção entre ambas (dentro da esfera e acima do cone). Vamos fazer a superfície de teto menos a de baixo:

f x , y = 1 - x 2 - y 2 - x 2 + y 2

Logo:

V = ∬ R 1 - x 2 - y 2 - x 2 + y 2 d x d y

Porém já temos em mente que precisamos fazer a mudança para coordenadas polares:

f x , y = 1 - x 2 - y 2 - x 2 + y 2

f r , θ = 1 - r 2 c o s 2 θ - r 2 s e n 2 ( θ ) - r 2 c o s 2 θ + r 2 s e n 2 ( θ )

f r , θ = 1 - r 2 - r

Com isso:

V = ∬ R 1 - x 2 - y 2 - x 2 + y 2 d x d y = ∬ R 1 - r 2 - r r d r d θ

Agora precisamos determinar os intervalos de integração.

Passo 3

Vamos começar pelo r :

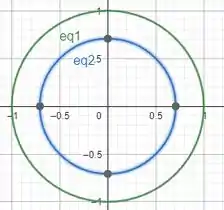
No caso, como queremos o raio até a intercepção entre as superfícies, teremos

0 ≤ r ≤ 1 2

Agora vamos encontrar θ . No caso, reparem que vai completar uma circunferência completa, então

0 ≤ θ ≤ 2 π

Logo

V = ∬ R 1 - r 2 - r r d r d θ = ∫ 0 2 π ∫ 0 1 2 1 - r 2 - r r d r d θ

Agora podemos calcular.

Passo 4

Agora vamos resolver a nossa integral:

V = ∫ 0 2 π ∫ 0 1 2 1 - r 2 - r r d r d θ = ∫ 0 2 π ∫ 0 1 2 r 1 - r 2 - r 2 d r d θ

Começando pela mais interna:

∫ 0 1 2 r 1 - r 2 - r 2 d r = - 1 3 1 - r 2 3 2 - r 3 3 0 1 2

∫ 0 1 2 r 1 - r 2 - r 2 d r = 1 3 - 1 3 2

Ficando agora

V = ∫ 0 2 π ∫ 0 1 2 r 1 - r 2 - r 2 d r d θ = ∫ 0 2 π 1 3 - 1 3 2 d θ

Vamos integrar a última:

V = ∫ 0 2 π 1 3 - 1 3 2 d θ = θ 3 - θ 3 2 0 2 π

V = ∫ 0 2 π 1 3 - 1 3 2 d θ = 2 π 3 1 - 1 2

Resposta

2 π 3 1 - 1 2

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}