UNICAMP – Sem campus – Cálculo 2 – P2 – 5º tarde - 2
Calcule a integral
Onde .
Passo 1
Fala turminha, tudo em cima? Bora lá resolver essa questão. Ela pode parecer fácil e difícil ao mesmo tempo. Fácil porque tem uma integral ali que parece simples né? Apenas um inofensivo. Porém, a parte chata dela está nesse . Vamos dar nome aos bois então. Esse , é um domínio. E é justamente esse domínio que vai limitar a nossa região de integração. Mas agora vamos olhar pra equação que ele nos entrega pra gente como domínio:
.
No próximo passo a gente abre essa coisa enorme aí 😊
Passo 2
Vocês sabem como a gente lê isso? Vou simplificar pra vocês: O domínio da nossa função está limitado (dentro do plano ) por:
E por:
Hm... como a gente vê isso graficamente? Bem, a primeira função me lembra muito o formato de uma elipse. No gráfico, ela fica da seguinte forma:
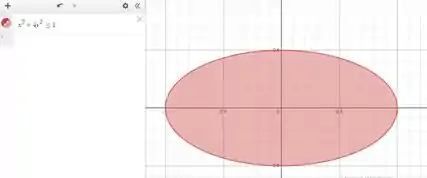
Que fofinha
Isso quer dizer que representa somente a parte positiva (no eixo ), portanto, vamos considerar somente a parte azul escura do gráfico:
Passo 3
Belezinha, demos nome aos bois. Agora vamos traduzir esses intervalos que a integral nos deu para . Logo,
Isolando , para encontrarmos o intervalo de limita a nossa elipse:
Como é o módulo de , entendemos que os limites de integração são:
Daí, podemos escrever dessa forminha mais formal:
Passo 4
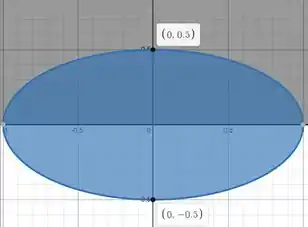
Respira aí que tamo quase lá! Agora que temos os limites de integração em , precisamos achar os limites de integração em . Mas se você tiver o olho de tandera, a gente já achou esses limites quando desenhamos nossa elipse:
Para acharmos os limites de , basta calcular os intervalos da elipse quando , que é o centro da elipse. Logo:
Logo, eixo está limitado por e por .
Passo 5
Armando nossa integral, temos então:
Agora é cair pra cima das integrais! Resolvendo a primeira, por definição temos que:
Portanto:
Levando isso dentro da segunda integral em :
Agora é resolver esse monstrinho! Já indo pra resolução pra não perdermos muito tempo, temos que: