Questão 2. Use técnicas de integração para determinar a área da região plana delimitada pelos círculos e e que está entre as retas e .
Passo 1
Pow, a essa altura do campeonato, uma área de uma região plana, , é uma integral dupla:
Então, se vamos calcular uma integral dupla em cima de , vale muito a pena enxergar esse essa região , primeiro, certo? Logo, siga-me!
Passo 2
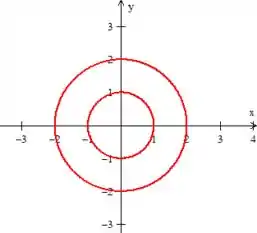
Para desenhar essa região, basta colocar no plano essas curvas delimitadoras. A duas primeiras são circunferências, uma de raio e outra de raio :
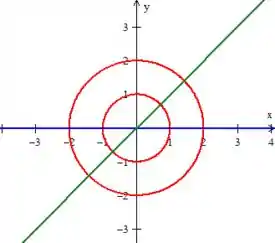
Tem duas retas que delimitam essa região também, (em azul) e (em verde)...
Logo, a região que queremos está entre essas curvas são esses dois pedacinhos aqui:
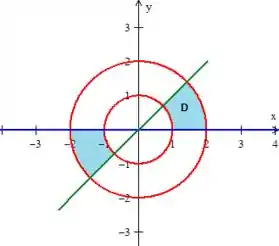
Sacou? Como esses dois pedacinhos são iguais, podemos calcular a área desse pedacinho :
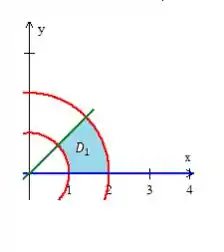
e depois multiplicar por dois !
Passo 3
Bem, estamos trabalhando dentro de circunferências, então vamos utilizar as coordenas polares:
E não podemos deixar de considerar o Jacobiano dessa brincadeira:
Como toda mudança, devemos buscar a variação dos novos caras, no caso e .
varia de uma circunferência a outra. Como a raio da menor é e da maior é ...
Em relação ao ... Se olharmos novamente para a região, sabendo que é o ângulo que sai do eixo e gira no sentido anti-horário...
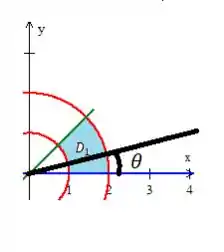
A reta verde tem equação
Substituindo as polares...
Que ângulo tem a tangente igual a ?
Portanto ...
Passo 4
Finalmente, com as informações de variação das nossas variáveis:
Podemos voltar para a integral dupla:
E substituir tudo, não se esquecendo de multiplicar pelo módulo do Jacobiano que encontramos:
Integrando em ...
Passo 5
Como a área da Região é o dobro da Área da região ...