Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 991234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798100

Enunciado

  1. Calcule a integral abaixo

∬ R cos ⁡ x 2 + y 2 d x d y

Onde R   é o círculo de centro 0,0 e raio π / 2 .

Passo 1

Oi, galerinha! Tudo bom? Aqui temos um integralzinha para resolver, porém ele não deu os limites de integração. Só sabemos que ela está limitada na região R , que está dentro do círculo de centro 0,0 e raio π / 2

Então vamos começar desenhando essa região para encontrar os limites de integração.

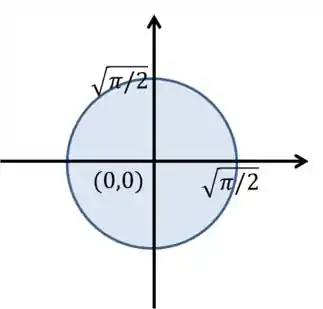
Como queremos apenas o primeiro quadrante, a nossa região é parte preenchida do circulo na área vermelha.

Agora vamos achar os nossos limites de integração e montar a intregal.

Passo 2

Antes de montar a integral, aqui vai uma dica para vocês: sempre que a nossa região tiver o formato de uma circunferência e tivermos na nossa função um x 2 + y 2 , vamos usar coordenadas polares.

Pelas coordenadas polares, nós integramos em função de r e θ . Então vamos achar os novos limites integração

Como estamos dando uma volta completa, temos θ varia de 0 até 2 π e raio r de 0   até π / 2 .

Além disso, vamos fazer a seguinte mudança de variável:

x = r cos ⁡ θ

y = r sin ⁡ θ

Logo,

x 2 + y 2 = r cos ⁡ θ 2 + r sin ⁡ θ 2

x 2 + y 2 = r 2 cos 2 ⁡ θ + sin 2 ⁡ θ

Pela identidade trigonométrica, temos que cos 2 ⁡ θ + sin 2 ⁡ θ = 1 . Ou seja,

x 2 + y 2 = r 2

Agora vamos montar a integral!

Passo 3

Galerinha! Para quem achou que já podemos montar a nossa integral: CUIDADO! Sempre que fizermos uma mudança de coordenada, temos que calcular o nosso Jacobiano.

A gente vai precisar calculá-lo usando a fórmulinha do jacobiano J :

J = ∂ ( x , y ) ∂ ( r , θ ) = ∂ x ∂ r ∂ x ∂ θ ∂ y ∂ r ∂ y ∂ θ

Vamos substituir nossas expressões para x e y ali:

J = ∂ r cos ⁡ θ ∂ r ∂ r cos ⁡ θ ∂ θ ∂ r   s e n   θ ∂ r ∂ r   s e n   θ ∂ θ

J = cos ⁡ θ - r   s e n θ s e n   θ r   c o s   θ = r   c o s 2 θ + r   s e n 2 θ = r [ c o s 2 θ + s e n 2 θ ]

J = r

Agora sim podemos montar a nossa integral!

Passo 4

A gente tinha,

∬ R cos ⁡ x 2 + y 2 d x d y

Mudamos o integrando para

∬ R r   cos ⁡ x 2 + y 2 d x d y

Aí a gente substitui as expressões da mudança de variáveis nesse integrando para que ele fique só em r e θ . Vamos usar x 2 + y 2 = r 2

∬ R   r cos ⁡ x 2 + y 2 d x d y =   ∬ R r  cos ⁡ r 2 d r d θ

Para finalizar, a gente coloca nossos extremos de integração:

0 ≤ r ≤ π / 2

0 ≤ θ ≤ 2 π

Como as duas variáveis estão entre números, não importa a ordem em que vamos montar. Vamos escolher integrar primeiro em relação a r , aí a integral de dentro tem os extremos de r e o diferencial d r , e a integral de fora tem os extremos de θ e o diferencial d θ :

∫ 0 2 π ∫ 0 π / 2 r cos ⁡ r 2 d r d θ

Agora bora resolver a integral!

Passo 5

Toda integral dupla nós sempre resolvemos de dentra para fora. Ou seja, primeiro vamos integrar em função de r e depois integraremos em função de θ .

Sendo assim, a primeira integral que temos que resolver é

∫ 0 π / 2 r cos ⁡ r 2 d r

Para isso, vamos usar uma mudança de variável,

u = r 2

d u = 2 r d r → d u 2 = r d r

Logo,

∫ r cos ⁡ r 2 d r = ∫ cos ⁡ u d u 2

E

∫ cos ⁡ u d u 2 = - 1 2 sin ⁡ u

Voltando para variável r , ficamos com

∫ r cos ⁡ r 2 d r = - 1 2   sin ⁡ r 2

Colocando os limites de integração, ficamos com

∫ 0 π / 2 r cos ⁡ r 2 d r = - 1 2   sin ⁡ r 2 | π / 2 0 = - 1 2 sin ⁡ π 2 2 - sin ⁡ 0 2 = 1 2

Agora vamos para segunda integral!

Passo 6

Ficamos com

∫ 0 2 π ∫ 1 π / 2 r cos ⁡ r 2 d r d θ = ∫ 0 2 π 1 2 d θ

= 1 2 θ | 2 π 0 = 1 2 2 π = π

Resposta

π

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}