UFABC. Cálculo. Funções de Várias Variáveis. Lista 6 - Integrais Duplas. Questão 7f.
7 - Usando coordenadas polares, calcule:
f) , onde é a região limitada por .
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Quando estamos calculando integrais e nos deparamos com uma integral onde temos que calcula-la a partir de uma região de integração circular ou elíptica, o que temos que fazer é converter nossas coordenadas e para coordenadas polares.
Ok, mas como fazemos isso?? 🤔
Como nossa região de integração é circular, temos que trocar por e por . Dessa forma, vamos converter nossa função para e ao invés de integrarmos , vamos integrar onde é a variação do raio e é a variação angular da região com relação à origem do sistema.
Entendeu? Bora começar!
Passo 2
Primeiro de tudo, vamos ver como é nossa região .
Se o limite de é , então
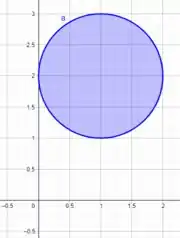
Observando nossa função de integração vemos que estamos tratando de uma circunferência também centrada em .
Se tentássemos encontrar o valor pra , íamos chegar em algo mirabolante. Então usando nossa expertise de futuros engenheiros podemos pensar “e se transladássemos o centro da nossa origem?” assim, poderíamos calcular essa integral de uma maneira muito mais fácil.
Partindo dessa ideia, como o centro da nossa função está em , podemos dizer que e
Dessa forma que movemos o centro do nosso sistema para a posição .
Agora continuamos os cálculos normalmente.
Vamos encontrar os limites de integração para .
Como , temos
Com isso, descobrimos que os limites de integração em é de a .
Bacana, não é? 😁
Passo 3
Como nossa região é um círculo completo e transladamos nossa origem para seu centro, nossa variação em é de a .
Agora temos que converter nossa função de integração, temos
Simplificando o resultado
Essa mudança não afeta nosso jacobiano, então nossa integral é dada por
Agora temos uma integral que sabemos resolver, não é?
Integrando primeiramente com relação a pelo método de integração polinomial onde dividimos a variável pela sua potência e somamos no seu expoente.
Aplicando os limites de integração
Tranquilo até aqui?
Passo 4
Agora vamos integrar o resultado que obtemos em relação a .
Como nossa função de integração é uma constante, sabemos que a integral de uma constante é a própria constante multiplicada pela variável de integração.
Aplicando os limites de integração, temos
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
