Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 401234567891011121314151617181920212223242526272829303132333435363738394142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

(4) Seja R a região contida no primeiro quadrante do plano, limitada pela curva x 2 + y 2 = 9 , pela reta y = 3 x e pela reta x = 0 . Marque a opção que representa a integral ∬ R     x   d x d y após mudar para coordenadas polares.

  1. ∫ π / 3   π / 2   ∫ 0 3   r 2 cos ⁡ θ d r d θ
  2. ∫ π / 6 π / 2 ∫ 0 3   r 2 cos ⁡ θ d r d θ
  3. ∫ π / 3 π / 2 ∫ 0 3   r cos ⁡ θ d r d θ
  4. ∫ π / 6   π / 2 ∫ 0 3   r cos ⁡ θ d r d θ
  5. ∫ 0 π / 3 ∫ 0 3   r 2 cos ⁡ θ d r d θ

Passo 1

Bem, em exercícios como esse, vamos, em primeiro lugar, desenhar essa região R .

Sabemos que estamos no primeiro quadrante dentro de uma circunferência de raio 3 , x 2 + y 2 = 9 :

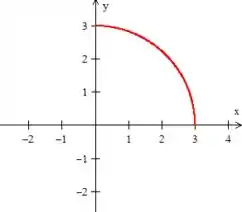
Temos uma reta passando pela origem y = 3 x ...

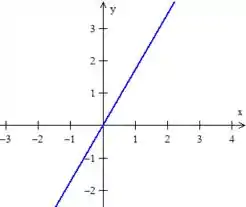
E, além disso, nossa região também está delimitada pela reta x = 0 ...

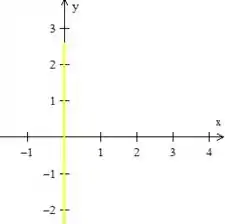
Logo a região que estamos trabalhando é esse pedacinho de pizza aqui, oh:

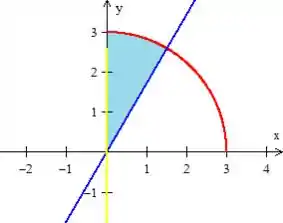
Passo 2

Como o problema nos pediu, devemos fazer uma mudança para as coordenadas polares:

x = r cos ⁡ θ

y = r sin ⁡ θ

Só que não podemos esquecer que uma mudança nos exige que multipliquemos pelo Jacobiano que no caso das polares é:

J = r

Agora, como toda e boa mudança, devemos buscar os limites dos novos caras!

Passo 3

Para o limite de r , bem... Ele está variando da origem, até o raio da borda da “pizza” ou melhor da circunferência vermelha:

0 ≤ r ≤ 3

Já o θ , bem, lembrando que o θ é esse ângulo que inicia no eixo x e gira no sentido anti-horário assim:

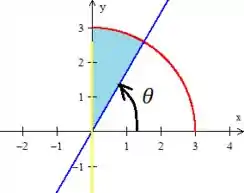
Percebemos que no caso o ângulo θ inicia na reta azul e vai até o ângulo de 90 ° ...

R e t a   a z u l ≤ θ ≤ π 2

A reta azul é:

y = 3 x

substituindo as coordenadas polares...

r sin ⁡ θ = 3   r cos ⁡ θ       →

r sin ⁡ θ r cos ⁡ θ = 3                   →        

tan ⁡ θ = 3

Logo, o θ só pode nesse caso ser de 60 ° ...

π 3 ≤ θ ≤ π 2

Passo 4

Com esses dois intervalos:

π 3 ≤ θ ≤ π 2

0 ≤ r ≤ 3

Podemos remontar a integral dupla, mas não se esquecendo de multiplicar a função pelo Jacobiano:

∬ R     x   d x d y = ∫ π 3 π 2 ∫ 0 3 r cos ⁡ θ ⋅ J   d r d θ =

∫ π 3 π 2 ∫ 0 3 r 2 cos ⁡ θ   d r d θ

Resposta

a )     ∫ π / 3   π / 2   ∫ 0 3   r 2 cos ⁡ θ d r d θ

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}