Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 301234567891011121314151617181920212223242526272829313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

  1. Passe para coordenadas polares e calcule:

∫ 1 3 ∫ 0 y 1 x 2 + y 2   d x d y

Passo 1

Bem, a primeira coisa aqui é tentar entender um pouco melhor sobre a própria região que estamos querendo trabalhar.

A única informação que temos sobre a região é dada pela própria integral afinal de contas sabemos que:

1 ≤ y ≤ 3

0 ≤ x ≤ y

Pow! Com essa primeira inequação, ganhamos:

y = 1

y = 3

x = 0

x = y

Colocando essas quatro equações em um plano, obtemos essas quatro retas:

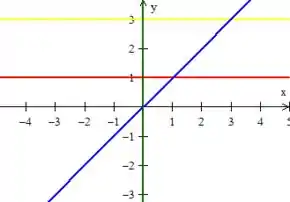
Onde logo obtemos a região, no interior delas

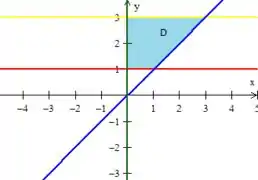
Passo 2

Como o próprio problema nos pediu, devemos mudar então para as famosas coordenadas polares, onde vamos fazer a seguinte troca:

x = r cos ⁡ θ

y = r sin ⁡ θ

x 2 + y 2 = r 2

Não se esqueça do Jacobiano:

J = r

Pois bem! Toda e qualquer mudança que fazemos temos que determinar quais são os limites dos novos camaradas (no caso é o r e θ ). Bora?

Passo 3

Agora preciso de muita atenção sua, pois o ângulo θ , como ele gira saindo do eixo x dessa forma

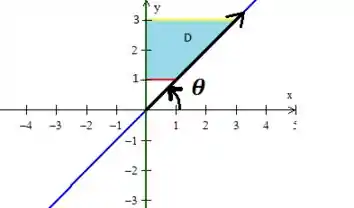
vamos obter seus limites usando a reta de entrada do ângulo, y = x e a reta de saída que é x = 0 . Como?! Não se preocupe, pois basta substituir as polares nessas duas retas . Veja!

x = y         →           r cos ⁡ θ = r sin ⁡ θ

cortando o r dos dois lados...

cos ⁡ θ = sin ⁡ θ

Agora quando o cosseno é igual ao seno no primeiro quadrante? Exatamente! Quando o ângulo é de 45   ° , sacou? Logo o ângulo inicial é de π 4 .

Para o ângulo de saída...

x = 0             →                 r cos ⁡ θ = 0

como o r é positivo...

cos ⁡ θ = 0

Então o ângulo θ de saída só pode ser de 90   ° logo a gente pode afirmar que...

π 4 ≤ θ ≤ π 2

Passo 4

Muito bem! Agora vamos descobrir a variação do raio usando essas duas retas horizontais, pois o raio sempre entra em uma e sai na outra, saca? (Acompanhe com o seu dedo, a reta preta para você ver onde o raio entra e sai experimentalmente haha !

Utilizando a reta vermelha (de entrada)...

y = 1     ⇒ S u b s t i t u i n d o   p e l a f o r m a   p o l a r                 r sin ⁡ θ = 1

Isolando o r ...

r = 1 sin ⁡ θ = cossec ⁡ θ

Agora com a reta amarela de saída...

y = 3           →                 r sin ⁡ θ = 3

r = 3 sin ⁡ θ = 3 cossec ⁡ θ

Passo 5

Com esses dados de variação em mãos

cossec ⁡ θ ≤ r ≤ 3 cossec ⁡ θ

π 4 ≤ θ ≤ π 2

podemos então agora montar a integral simplesmente substituindo tudo (não esqueça de multiplicar pelo Jacobiano quando realizar a troca)

∫ 1 3 ∫ 0 y 1 x 2 + y 2   d x d y = ∫ π 4 π 2 ∫ cossec ⁡ θ 3   cossec ⁡ θ 1 r 2 ∙ r   d r d θ =

∫ π 4 π 2 ∫ cossec ⁡ θ 3   cossec ⁡ θ   d r d θ

Agora é só integrar! Bora?

Passo 6

Resolvendo então a integral de dentro:

∫ π 4 π 2 ∫ cossec ⁡ θ 3   cossec ⁡ θ   d r d θ = ∫ π 4 π 2 ∫ cossec ⁡ θ 3   cossec ⁡ θ   d r d θ =

∫ π 4 π 2   r cossec ⁡ θ 3   cossec ⁡ θ d θ

substituindo os limites...

∫ π 4 π 2   r cossec ⁡ θ 3   cossec ⁡ θ d θ = ∫ π 4 π 2 3 cossec ⁡ θ - cossec ⁡ θ d θ =

∫ π 4 π 2 2 cossec ⁡ θ d θ

Passando esse dois pra fora...

2 ∫ π 4 π 2 cossec ⁡ θ d θ

Agora aqui eu preciso muito que você se recorde dessa integral (ela é uma das que temos que memorizar, lembra?)

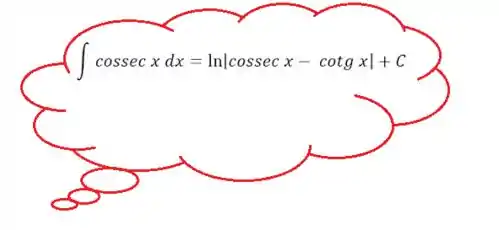
Logo...

2 ∫ π 4 π 2 cossec ⁡ θ d θ = 2   ln ⁡ cossec ⁡ θ - cotg ⁡ θ π 4 π 2 =

substituindo...

2 ln ⁡ cossec ⁡ π 2 - cotg ⁡ π 2 - ln ⁡ cossec ⁡ π 4 - cotg ⁡ π 4 =

2 ln ⁡ 1 - 0 - ln ⁡ 2 - 1 =

- 2 ln ⁡ 2 - 1

Resposta

c )     - 2 ln ⁡ 2 - 1

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}