Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 521234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFABC. Cálculo. Funções de Várias Variáveis. Lista 6 - Integrais Duplas. Questão 10.

10 - Calcule a área da elipse x 2 + 4 y 2 - 4 x = 0 .

Passo 1

Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍

Essa questão foi bem direta com a gente. O objetivo é calcular a área da elipse dada pela equação x 2 + 4 y 2 - 4 x = 0 .

Mas então você deve pensar: “ah! É só aplicar a fórmula da área da elipse que está tudo certo!”

Mas aposto que se fizermos isso seu professor vai ficar

Nessa lista, estamos estudando integrais duplas, então temos que obter essa área através desse método.

Como estando lidando com uma elipse, temos que integrar usando coordenadas polares. Para elipses temos algumas particularidades, por exemplo, para a equação de uma elipse

x 2 a 2 + y 2 b 2 = 1

Temos que substituir x por a r c o s θ e y por b r s e n θ . Já nosso jacobiano é dado por j = a b r .

Entendeu as diferenças? Vamos começar!

Passo 2

Primeiro, vamos organizar nossa equação

x 2 + 4 y 2 - 4 x = 0

Se adicionarmos 4 dos dois lados da equação, podemos fazer o seguinte

x 2 - 4 x + 4 + 4 y 2 = 4

Você concorda que x 2 - 4 x + 4 = x - 2 2 ? Logo

x - 2 2 + 4 y 2 = 4

Dividindo os dois lados por 4 , temos

x - 2 2 4 + y 2 1 = 1

Essa equação é de uma elipse com o centro deslocado onde a = 2 e b = 1 .

Quando temos o centro deslocado para calcular a área, podemos considerar x - 2 onde antes definimos nosso x , ou seja, antes substituímos x por a r c o s θ , agora substituímos x - 2 por a r c o s θ .

Com isso, estamos transladando a origem do nosso sistema para o centro da nossa elipse.

Esboçando nossa equação, podemos visualizar nossa região

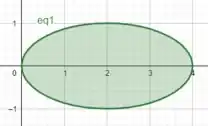
Tranquilo até aqui? 👀

Passo 3

Vamos converter nossa equação para polar e ver como podemos definir r e θ da nossa integral.

2 r c o s θ 2 4 + 1 r s e n θ 2 1 = 1

4 r 2 c o s 2 θ 4 + r 2 s e n 2 θ = 1

r 2 c o s 2 θ + r 2 s e n 2 θ = 1

Colocando r 2 em evidencia e lembrando que c o s 2 θ + s e n 2 θ = 1 , temos

r 2 c o s 2 θ + s e n 2 θ = 1

r 2 = 1

r = 1

Já θ é obtido analisando o ângulo que nossa região de integração faz com nossa origem do sistema. Como transladamos nossa origem para o centro da elipse, toda a volta da nossa origem tem região da elipse, logo θ faz a volta completa.

Com essas informações, vemos que os limites de integração de d r vai de 0 a 1 e os limites de integração em d θ de 0 a 2 π .

Como queremos calcular a área de uma região, nossa função de integração é 1 (sem esquecer do nosso jacobiano j = 2 r ), ou seja

∫ 0 2 π ∫ 0 1 1 2 r d r d θ

∫ 0 2 π ∫ 0 1 2 r d r d θ

Bora começar a calcular nossa integral? 😁

Passo 4

Primeiro vamos integrar com relação a r . Nesse caso, a integral é obtida pelo método de integração polinomial onde dividimos a variável pela sua potência + 1 e somamos 1 no seu expoente.

∫ 2 r d r = 2 r 1 + 1 1 + 1 = r 2

Aplicando os limites de integração, temos

∫ 0 1 2 r d r = 1 2 - 0 2

∫ 0 1 2 r d r = 1

Agora com base nesse resultado, integramos com relação a θ . Como nossa nova função de integração é uma constante, sabemos que a integral de uma constante é a própria constante multiplicada pela variável de integração.

∫ 1 d θ = θ

Aplicando os limites de integração

∫ 0 2 π 1 d θ = 2 π - 0

Logo, o resultado é dado por

∫ 0 2 π ∫ 0 1 2 r d r d θ = 2 π

Comparando o resultado com a formula da área da elipse, temos

A = a · b · π

A = 2 π

E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí

Resposta

∫ 0 2 π ∫ 0 1 2 r d r d θ = 2 π

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}