Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 131234567891011121415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFSCAR, Sem Campus, Cálculo 3, Listas de C3 - Profª Alessandra Verri - Lista 3, Questão 1c

Por meio de coordenadas polares, calcule a integral

∬ R x 2 + y ² d A

Em que R é a região limitada pelo triângulo de vértices 0,0 ,   3,0   e   ( 3,3 ) .

Passo 1

Bom, para começar galera, a gente precisa encontrar a região limitada. Para isso, vamos marcar no plano cartesiano os pontos e delimitar a região. Vamos dizer que:

A = 0,0

B = 3,0

C = ( 3,3 )

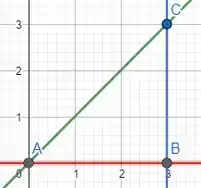
Show, região delimitada. E por meio dela vamos determinar os intervalos de integração.

Passo 2

Vamos começar encontrando os intervalos em relação a x :

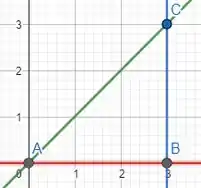
Olhando para o nosso plano cartesiano e os pontos dele, vamos dizer que:

0 ≤ x ≤ 3

Passo 3

Agora vamos determinar o intervalo de integração em relação a y . Como a gente afirmou que o intervalo de x varia entre números, y vai variar entre funções. Então temos que achar as funções de cada reta ali.

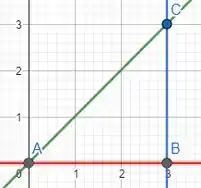
Para começar, vamos determinar a função principal da reta AC.

y = m x + b

Baseado nos pontos A e C :

A → 0 m + b = 0 C → 3 m + b = 3

A → b = 0 C → m = 1

Logo:

y = x

Com isso, o intervalo de integração de y :

0 ≤ y ≤ x

Passo 4

Agora que conseguimos achar os intervalos de integração, podemos substituir na integral:

∬ R x 2 + y ² d A = ∫ 0 3 ∫ 0 x x 2 + y ² d y d x

Show, mas o enunciado fala com a gente para usar coordenadas polares, então teremos que fazer essa alteração. Para isso, vamos usar:

x = r c o s ( θ )

y = r s e n ( θ )

J = r

Substituindo:

∫ 0 3 ∫ 0 x x 2 + y ² d y d x = ∫ 0 3 ∫ 0 x r ² c o s ² ( θ ) + r 2 s e n 2 ( θ ) r d θ d r

Vamos começar encontrando θ . Para isso, temos que achar o ângulo que a reta forma com o eixo x

t a n θ = 3 3 = 1 → θ = 45 º = π 4

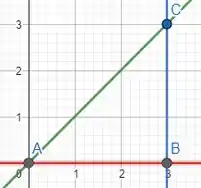
Logo

0 ≤ θ ≤ π 4

Agora vamos encontrar o intervalo de r :

y = 0 → r s e n θ = 0

r = 0

Olhando para o outro ponto agora

y = 3 → r s e n θ = 3

r = 3 s e n θ = 3 c o s s e c ( θ )

Logo o intervalo:

0 ≤ r ≤ 3 c o s s e c ( θ )

Substituindo a integral:

∫ 0 3 ∫ 0 x x 2 + y ² d y d x = ∫ 0 π 4 ∫ 0 3 c o s s e c ( θ ) r ² c o s ² ( θ ) + r 2 s e n 2 ( θ ) r d r d θ

∫ 0 3 ∫ 0 x x 2 + y ² d y d x = ∫ 0 π 4 ∫ 0 3 c o s s e c ( θ ) r ² d r d θ

Agora podemos resolver:

∫ 0 3 ∫ 0 x x 2 + y ² d y d x = ∫ 0 π 4 ∫ 0 3 c o s s e c ( θ ) r ² d r d θ

∫ 0 3 ∫ 0 x x 2 + y ² d y d x = 1 3 ∫ 0 π 4 ( r 3 ) 0 3 c o s s e c ( θ ) d θ

∫ 0 3 ∫ 0 x x 2 + y ² d y d x = 9 ∫ 0 π 4 c o s s e c 3 θ d θ

Agora resolvendo a outra integral:

∫ 0 3 ∫ 0 x x 2 + y ² d y d x = 9 ∫ 0 π 4 c o s s e c 3 θ d θ

∫ 0 3 ∫ 0 x x 2 + y ² d y d x = 9 2 2 + ln ⁡ 2 + 1

Resposta

∫ 0 3 ∫ 0 x x 2 + y ² d y d x = 9 2 2 + ln ⁡ 2 + 1

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}