Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 461234567891011121314151617181920212223242526272829303132333435363738394041424344454748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Calcule a área da região D situada fora do círculo de equação x 2 + y 2 = 9 e dentro do círculo de equação x 2 + y 2 - 6 y = 0

Passo 1

Simbora começar entendendo qual a região que queremos calcular a área.

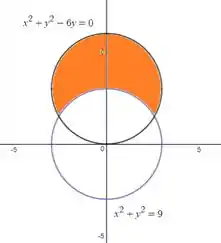
Bom, então ficamos com a região laranja marcada.

Passo 2

Queremos calcular a área, que é a integral dupla em outras palavras, e estamos trabalhando com circunferências, pra facilitar nossa vida, entram as coordenadas polares.

Show, então vamos fazer as mudanças, fazendo x = rcos ⁡ θ e y = r s e n θ e igualar as duas equações pra achar os pontos de encontro das circunferências e ver em que altura de θ eles ficam. Lembrando de o J = r .

x 2 + y 2 = 9 x 2 + y 2 = 6 y

r 2 = 9   → r = 3

r 2 = 6 r sen ⁡ θ → r = 6 s e n θ  

Igualando as equações:

3 = 6 s e n θ

a r c s e n 1 2 = θ

θ = π 6   e 5 π 6

Isso significa então que os pontos de encontro das circunferências estão em   θ = π 6   e 5 π 6 .

Passo 3

Como a gente quer a área, ficamos com

∬ D 1 d A

Fazendo as substituições e não esquecendo do nosso amigo Jacobiano a gente fica com

∫ π 6 5 π 6 ∫ 3 6   s e n θ r   d r d θ

∫ π 6 5 π 6 r 2 2 3 6 s e n θ d θ

1 2 6 s e n θ 2 - 9 = 36 s e n 2 θ - 9 2 = 27 s e n 2 θ + 9 s e n 2 θ - 9 2

Veja que: 9 s e n 2 θ - 9 = 9 s e n 2 θ - 1 = - 9 cos 2 ⁡ θ . Substituindo:

∫ π 6 5 π 6 r 2 2 3 6 s e n θ d θ = ∫ π 6 5 π 6 27 s e n 2 θ - 9 cos 2 ⁡ θ 2 d θ = 9 ∫ π 6 5 π 6 3 s e n 2 θ - cos 2 ⁡ θ 2 d θ

Ok, agora veja ainda que:

cos ⁡ 2 θ = cos 2 ⁡ θ - s e n 2 θ

- cos ⁡ 2 θ = s e n 2 θ - cos 2 ⁡ θ

Entao:

9 ∫ π 6 5 π 6 2 s e n 2 θ - cos ⁡ 2 θ 2 d θ

Por último: s e n 2 θ = 1 - cos ⁡ 2 θ 2 . Então:

9 ∫ π 6 5 π 6 1 - cos ⁡ 2 θ - cos ⁡ 2 θ 2 d θ = 9 ∫ π 6 5 π 6 1 - 2 cos ⁡ 2 θ 2 d θ

9 θ 2 π 6 5 π 6 - sin ⁡ 2 θ 2 π 6 5 π 6

9 θ 2 - 9 2 s e n 2 θ π 6 5 π 6

3 π + 9 2 3

Resposta

3 π + 9 2 3

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}