Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 311234567891011121314151617181920212223242526272829303233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

  1. Uma placa D tem a forma da região limitada pelas retas x = 1 , x = 2 , y = 0 e y = x 3 .

A densidade em cada ponto é inversamente proporcional a distância à distância do ponto à origem. Determine a massa da placa.

Passo 1

Pow! Massa de uma região a essa altura do campeonato para você tem que ser uma integral dupla:

M a s s a D = ∬ D   δ x ,   y d x d y

Repare então que a nossa primeira missão é justamente descobrir quem é a função de densidade δ x ,   y e a també a região D .

Bora começar buscando essa função aí?

Passo 2

Como o próprio exercício nos pediu, precisamos tomar o inverso da função distância do ponto a origem.

Cara! A distância entre dois pontos quaisquer é dada por essa raiz aqui, oh

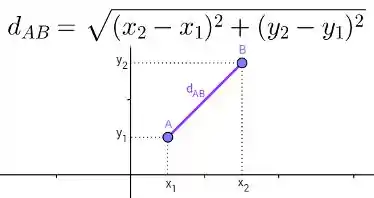
Lembrou-se dela?

Bem, mas no nosso caso, o ponto A é a origem, O = 0 ,   0 , e o ponto B é um ponto qualquer dentro da região, ( x ,   y )

d O B = x - 0 2 + y - 0 2 = x 2 + y 2

A função de densidade é inversamente proporcional a essa distância

δ x ,   y = k ∙ 1 x 2 + y 2

Onde k é uma constante de proporcionalidade, sacou?

Passo 3

Bem, quanto à região D precisamos desenha-la no plano. basta colocar todas essas 4 curvas no plano X Y :

  • x = 1 e x = 2 são retas paralelas ao eixo y :

  • y = 0 é o próprio eixo x

  • y = x 3 é uma reta que passa pela origem e tem mais ou menos essa cara aqui:

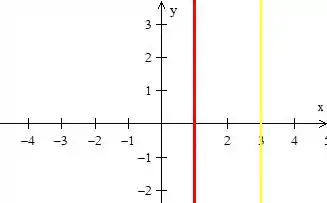
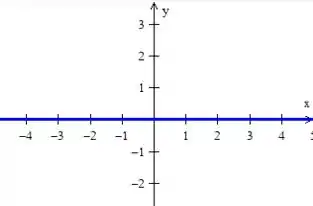
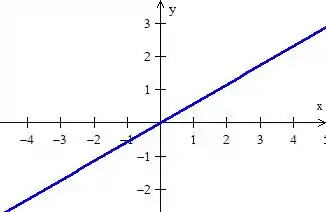
Logo, juntando essas 4 curvas já percebemos quem é a nossa região D :

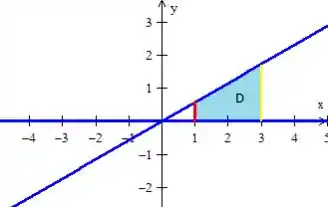
Passo 4

Pow! A nossa função é extremamente deselegante e envolve raiz de coisas ao quadrado o que nos sugere uma mudança para coordenadas polares :

x = r cos ⁡ θ

y = r sin ⁡ θ

Uma equação que nos ajuda muito é a equação da circunferência...

x 2 + y 2 = r 2

E, claro, o Jacobiano:

J = r

Agora, depois de uma mudança sempre buscamos quem são os limites de r e θ . Partiu?

Passo 5

Agora preciso de muita atenção sua, pois o ângulo θ , como ele gira saindo do eixo x dessa forma

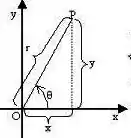
vamos obter seus limites usando a reta de entrada do ângulo, y = 0 e a reta de saída que é y = x 3 .

Como?!

Não se preocupe, pois basta substituir as polares nessas duas retas . Veja!

No caso do ângulo de entrada não precisa substituir, pois a gente já vê que ele é 0 °

Mas no caso do ângulo de saída a gente substitui na reta de saída...

y = x 3         →           r sin ⁡ θ = r cos ⁡ θ 3

cortando o r dos dois lados...

sin ⁡ θ = cos ⁡ θ 3

Bem, como o cosseno não zera até 90   ° o que sabemos estar bem longe neh haha, podemos passar esse cosseno dividindo...

sin ⁡ θ cos ⁡ θ = 1 3             →                 tan ⁡ θ = 1 3 = 3 3

Cara, que ângulo pode ser este daí? Sim! 30   °

Portanto...

0 ≤ θ ≤ π 6

Passo 6

Muito bem! Agora vamos descobrir a variação do raio usando essas duas retas verticais, pois o raio sempre entra em uma e sai na outra, saca? (Acompanhe com o seu dedo, a reta preta para você ver onde o raio entra e sai experimentalmente haha !

Utilizando a reta vermelha (de entrada)...

x = 1     ⇒ S u b s t i t u i n d o   p e l a f o r m a   p o l a r                 r cos ⁡ θ = 1

Isolando o r ...

r = 1 cos ⁡ θ = sec ⁡ θ

Agora com a reta amarela de saída...

x = 2           →                 r cos ⁡ θ = 2

r = 2 cos ⁡ θ = 2 sec ⁡ θ

Logo

L i n h a   V e r m e l h a ≤ r ≤ L i n h a   A m a r e l a

sec ⁡ θ ≤ r ≤ 2 sec ⁡ θ

Passo 7

Com esses dados de variação em mãos

sec ⁡ θ ≤ r ≤ 2 sec ⁡ θ

0 ≤ θ ≤ π 6

podemos então agora montar a integral simplesmente substituindo tudo (não esqueça de multiplicar pelo Jacobiano quando realizar a troca)

M a s s a D = ∬ D   δ x ,   y d x d y = ∬ D   k x 2 + y 2 d x d y =

∫ 0 π 6 ∫ sec ⁡ θ 2   sec ⁡ θ k r 2 ∙ r   d r d θ =

∫ 0 π 6 ∫ sec ⁡ θ 2   sec ⁡ θ k   d r d θ

Agora é só integrar! Bora?

Passo 8

Calculando então a integral de dentro...

∫ 0 π 6 ∫ sec ⁡ θ 2   sec ⁡ θ k   d r d θ = ∫ 0 π 6 ∫ sec ⁡ θ 2   sec ⁡ θ k   d r d θ =

Como k é uma constante, ela vaza das duas integrais

k ∫ 0 π 6 ∫ sec ⁡ θ 2   sec ⁡ θ   d r d θ =

k ∫ 0 π 6   r   sec ⁡ θ 2   sec ⁡ θ d θ =

integrando

k ∫ 0 π 6 2   sec ⁡ θ - sec ⁡ θ d θ = k ∫ 0 π 6 sec ⁡ θ d θ

Agora aqui eu preciso muito que você se recorde dessa integral (ela é uma das que temos que memorizar, lembra?)

∫ sec ⁡ x d x = ln ⁡ tan ⁡ θ 2 + π 4 + C

Logo...

k ∫ 0 π 6 sec ⁡ θ d θ = k ln ⁡ tan ⁡ θ 2 + π 4 0 π 6 =

substituindo...

k ln ⁡ tan ⁡ π 6 2 + π 4 - ln ⁡ tan ⁡ 0 2 + π 4 =

k ln ⁡ π 12 + π 4 - ln ⁡ tan ⁡ π 4 =

k ln ⁡ 3 - ln ⁡ 1 = k 2 ln ⁡ 3

Resposta

k 2 ln ⁡ 3

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}